题目内容
|
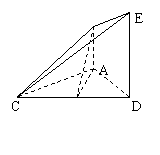（1） 求证：AF∥平面BCE；
（2） 求证：平面BCE⊥平面CDE．
|
取CE的中点G，连结BG、GF，因为F为
的中点，所以GF∥ED∥BA， GF＝
ED＝BA，
从而ABGF是平行四边形，于是AF∥BG. ……………………【4分】
因为AF
平面BCE，BG
平面BCE，所以AF∥平面BCE． ……………………【7分】
（2）因为AB⊥平面ACD，AF平面ACD，
所以AB⊥AF，即ABGF是矩形，所以AF⊥GF. ……………………【9分】
又AC=AD，所以AF⊥CD. ………………… 【11分】
而CD∩GF＝F，所以AF⊥平面GCD，即AF⊥平面CDE. 因为AF∥BG，所以BG⊥平面CDE.
因为BG平面BCE，所以平面BCE⊥平面CDE． ………………… 【14分】
练习册系列答案
名校课堂系列答案
相关题目
，其中
，若点P（1,1）在矩阵A的变换下得到点
，
,
,…
的10个零件，测量其直径（单位：cm），得到下面数据：
=
.
.从这6个一等品零件中随机抽取2个，所有可能的结果有：
,
,
,
,
,
,
共有15种.
，
，共有6种.
.
，∠BAD＝∠CDA＝45°.
（Ⅰ）求异面直线CE与AF所成角的余弦值； 
=
.
.从这6个一等品零件中随机抽取2个，所有可能的结果有：
,
,
,
,
,
,
共有15种.
，
，共有6种.
.
，∠BAD＝∠CDA＝45°.
（Ⅰ）求异面直线CE与AF所成角的余弦值； 
,
,…
的10个零件，测量其直径（单位：cm），得到下面数据：
=
.
.从这6个一等品零件中随机抽取2个，所有可能的结果有：
,
,
,
,
,
,
共有15种.
，
，共有6种.
.
，∠BAD＝∠CDA＝45°.
（Ⅰ）求异面直线CE与AF所成角的余弦值； 
=
.
.从这6个一等品零件中随机抽取2个，所有可能的结果有：
,
,
,
,
,
,
共有15种.
，
，共有6种.
.
，∠BAD＝∠CDA＝45°.
（Ⅰ）求异面直线CE与AF所成角的余弦值；