题目内容
(本题满分12分)已知定义在区间(0,+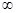 )上的函数,
)上的函数,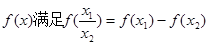 ,且当
,且当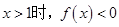 .① 求
.① 求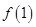 的值;② 判断
的值;② 判断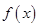 的单调性;③ 若
的单调性;③ 若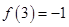 ,解不等式
,解不等式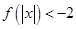 .
.
 )上的函数,
)上的函数,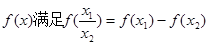 ,且当
,且当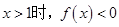 .① 求
.① 求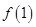 的值;② 判断
的值;② 判断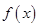 的单调性;③ 若
的单调性;③ 若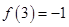 ,解不等式
,解不等式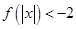 .
.解 ①令 ;②单调减函数
;②单调减函数
③, 。
。
 ;②单调减函数
;②单调减函数 ③,
 。
。本试题主要是考查了抽象函数的性质的运用,以及利用赋值法求解函数值和解不等式的综合运用。
(1)令x1=x2,得到f(1)的值。
(2)在第一问的基础上,设x1>x2>0,然后作差变形结合已知条件得到结论。
(3)因为f(3=-1,根据f(9)与f(3)的关系得到结论。
解 ① ,设
,设
②设 ,
,
 ,
, 为单调减函数
为单调减函数
③ ,即
,即 ,
, ,
, ,
, 单减函数,
单减函数, 。
。
(1)令x1=x2,得到f(1)的值。
(2)在第一问的基础上,设x1>x2>0,然后作差变形结合已知条件得到结论。
(3)因为f(3=-1,根据f(9)与f(3)的关系得到结论。
解 ①
 ,设
,设
②设
 ,
,
 ,
, 为单调减函数
为单调减函数③
 ,即
,即 ,
, ,
, ,
, 单减函数,
单减函数, 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

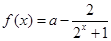 ,
,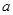 为何实数
为何实数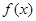 在定义域上总为增函数;
在定义域上总为增函数; 的定义域是 ( )
的定义域是 ( )



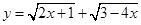 的定义域为( )
的定义域为( )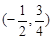
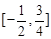
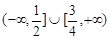
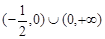
 在
在 上的最大值为3,最小值为2,则
上的最大值为3,最小值为2,则 的取值范围是 ( )
的取值范围是 ( )



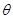 的始边
的始边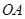 落在
落在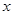 轴上,其始边、终边分别与单位圆交于点
轴上,其始边、终边分别与单位圆交于点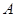 、
、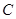 (
(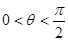 ),△
),△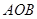 为等边三角形.
为等边三角形.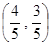 ,求
,求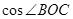 的值;
的值;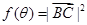 ,求函数
,求函数 的解析式和值域.
的解析式和值域.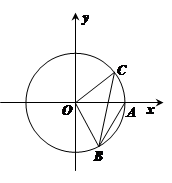
 的定义域为( ).
的定义域为( ). 



 的定义域为________.
的定义域为________.