题目内容
已知函数f(x)=ex-lnx,
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)在区间 内存在x0,使不等式f(x)<x+m成立,求m的取值范围.
内存在x0,使不等式f(x)<x+m成立,求m的取值范围.
解:(Ⅰ)函数f(x)的定义域为(0,+∞),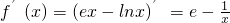
当f′(x)>0,即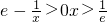 时,f(x)为单调递增函数;
时,f(x)为单调递增函数;
当f′(x)<0,即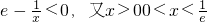 时,f(x)为单调递减函数;
时,f(x)为单调递减函数;
所以,f(x)的单调递增区间是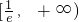 ,f(x)的单调递减区间是
,f(x)的单调递减区间是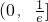
(Ⅱ)由不等式f(x)<x+m,得f(x)-x<m,令F(x)=f(x)-x,则F(x)=(e-1)x-lnx
由题意可转化为:在区间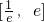 内,F(x)min<m,
内,F(x)min<m,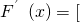 ,令F′(x)=0,得
,令F′(x)=0,得
由表可知:F(x)的极小值是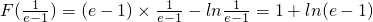 且唯一,
且唯一,
所以F(x)min=1+ln(e-1).因此,所求m的取值范围是(ln(e-1),+∞).
分析:(Ⅰ)先求出其导函数,以及导函数大于0,小于0对应的区间即可求函数f(x)的单调区间;
(Ⅱ)令F(x)=(e-1)x-lnx,先把问题转化为在区间 内,F(x)min<m;再利用导函数求出函数F(x)的单调性,进而求出其最小值即可求m的取值范围.
内,F(x)min<m;再利用导函数求出函数F(x)的单调性,进而求出其最小值即可求m的取值范围.
点评:本题第二问主要考查利用导函数来研究函数的极值.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.
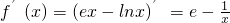
当f′(x)>0,即
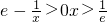 时,f(x)为单调递增函数;
时,f(x)为单调递增函数;当f′(x)<0,即
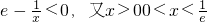 时,f(x)为单调递减函数;
时,f(x)为单调递减函数;所以,f(x)的单调递增区间是
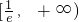 ,f(x)的单调递减区间是
,f(x)的单调递减区间是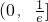
(Ⅱ)由不等式f(x)<x+m,得f(x)-x<m,令F(x)=f(x)-x,则F(x)=(e-1)x-lnx
由题意可转化为:在区间
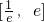 内,F(x)min<m,
内,F(x)min<m,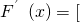 ,令F′(x)=0,得
,令F′(x)=0,得
| x |  | 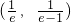 | 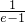 | 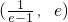 | e |
| F′(x) | - | 0 | + | ||
| F(x) | 递减 | 极小值 | 递增 |
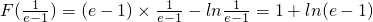 且唯一,
且唯一,所以F(x)min=1+ln(e-1).因此,所求m的取值范围是(ln(e-1),+∞).
分析:(Ⅰ)先求出其导函数,以及导函数大于0,小于0对应的区间即可求函数f(x)的单调区间;
(Ⅱ)令F(x)=(e-1)x-lnx,先把问题转化为在区间
 内,F(x)min<m;再利用导函数求出函数F(x)的单调性,进而求出其最小值即可求m的取值范围.
内,F(x)min<m;再利用导函数求出函数F(x)的单调性,进而求出其最小值即可求m的取值范围.点评:本题第二问主要考查利用导函数来研究函数的极值.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目