题目内容

已知数列{an}满足：a1=2，an=.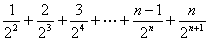

(Ⅰ)求证：数列{a2n+1}是等比数列；

(Ⅱ)记Sn=,若Sn≤t-恒成立，求正实数t的取值范围．

解:(Ⅰ)a2n+1=(a2n-1+1)+1=a2n-1+2 

=2a2n-2+2 

=2(a2n-2+1)

∴数列{a2n+1}是以a2+1=4为首项，2为公比的等比数列

(Ⅱ)由(Ⅰ)知，a2n+1=4·2n-1=2n+1

∴Sn=

∴Sn=

两式相减得 

=

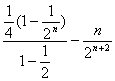
∴Sn=1-

∵对任意整数n均有Sn＜1

∴要使Sn＜t-  恒成立，当且仅当，x-≥1

解得t≥3   ∴t∈[3，+∞).

练习册系列答案
相关题目
已知数列{an}满足：a1=1且an+1=
3+4an
12-4an
， n∈N*．
（1）若数列{bn}满足：bn=
1
an-
1
2
(n∈N*)，试证明数列bn-1是等比数列；
（2）求数列{anbn}的前n项和Sn；
（3）数列{an-bn}是否存在最大项，如果存在求出，若不存在说明理由．
已知数列{an}满足
1
2
a1+
1
22
a2+
1
23
a3+…+
1
2n
an=2n+1则{an}的通项公式
 
．
已知数列{an}满足：a1=
3
2
，且an=
3nan-1
2an-1+n-1
（n≥2，n∈N*）．
（1）求数列{an}的通项公式；
（2）证明：对于一切正整数n，不等式a1•a2•…an＜2•n！
已知数列{an}满足an+1=|an-1|（n∈N*）
（1）若a1=
54
，求an；
（2）若a1=a∈（k，k+1），（k∈N*），求{an}的前3k项的和S3k（用k，a表示）
（2012•北京模拟）已知数列{an}满足an+1=an+2，且a1=1，那么它的通项公式an等于
2n-1
2n-1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网