题目内容
设平面点集M={(x,y)|(y-x)(y-
)>0} 其中k>0,N={(x,y)|x2+y2<4},则M∩N所表示的平面图形的面积为 .
| k | x |
分析:由集合A,B的式子的几何意义,作出A∩B如图所示的阴影部分,再利用圆和函数y=
的对称性即可求出面积.
| k |
| x |
解答: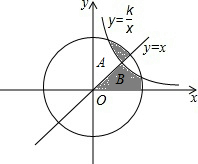 解:由N={(x,y)|x2+y2<4},
解:由N={(x,y)|x2+y2<4},
可知集合N表示的图形是以(0,0)为圆心,2为半径的圆内点集,
由(y-x)(y-
)>0,得
,或
,
∴集合A∩B所表示的平面图形为如图所示的阴影部分:
由圆和函数y=
的对称性可知:图中的A部分和B部分面积相等,
则S阴影=
×π×22=
,
故答案为:
 解:由N={(x,y)|x2+y2<4},
解:由N={(x,y)|x2+y2<4},可知集合N表示的图形是以(0,0)为圆心,2为半径的圆内点集,
由(y-x)(y-
| k |
| x |
|
|
∴集合A∩B所表示的平面图形为如图所示的阴影部分:
由圆和函数y=
| k |
| x |
则S阴影=
| 1 |
| 8 |
| π |
| 2 |
故答案为:
| π |
| 2 |
点评:此题考查了交集及其运算,以及简单的线性规划,正确找出可行域和利用对称性求面积是解题的关键.

练习册系列答案
相关题目