题目内容
已知函数 .
.
(1)设 的定义域为A,求集合A;
的定义域为A,求集合A;
(2)判断函数 在(1,+
在(1,+ )上单调性,并用单调性的定义加以证明.
)上单调性,并用单调性的定义加以证明.
 .
.(1)设
 的定义域为A,求集合A;
的定义域为A,求集合A;(2)判断函数
 在(1,+
在(1,+ )上单调性,并用单调性的定义加以证明.
)上单调性,并用单调性的定义加以证明.(1) ;(2)函数
;(2)函数 在
在 上单调递减.
上单调递减.
 ;(2)函数
;(2)函数 在
在 上单调递减.
上单调递减.试题分析:(1)由已知函数表达式为分式,故只须分母不为0即可,从而求得集合A;(2)根据函数单调性的定义法证明即可.
试题解析:(1)由
 ,得
,得 , 2分
, 2分所以,函数
 的定义域为
的定义域为 4分
4分(2)函数
 在
在 上单调递减. 6分
上单调递减. 6分证明:任取
 ,设
,设 , 则
, 则
 10分
10分

又
 ,所以
,所以 故
故
因此,函数
 在
在 上单调递减. 14分
上单调递减. 14分说明:分析
 的符号不具体者,适当扣1—2分.
的符号不具体者,适当扣1—2分.
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
 的定义域为 .
的定义域为 .
 的值域为 .
的值域为 . 的定义域为 ( )
的定义域为 ( )


 的定义域是
的定义域是 ,则函数
,则函数 的定义域是( ).
的定义域是( ). 



 的定义域为( )
的定义域为( )

 的值域为______________.
的值域为______________.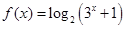 的值域为 .
的值域为 . 的定义域是( )
的定义域是( )