Question

已知抛物线y²=2px（p＞0）与双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）有相同的焦点F，点A是两曲线的一个交点，且AF⊥x轴，若l为双曲线的一条斜率大于

2

的渐近线，则l的斜率的取值范围是

{k|k=

2+2 2

}

．

Answer 1

分析：根据抛物线与双曲线有相同的焦点，得双曲线焦点为F（

p

2

，0）．如图，因为AF⊥x轴，点A（

p

2

，y₀）既在抛物线上又在双曲线上，所以由抛物线方程和双曲线方程组成方程组，联解得

b

a

=

2+2 2

，从而得到双曲线的斜率大于

2

的渐近线l方程为y=

2+2 2

x，由此即得l的斜率的取值范围．

解答：解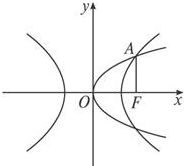：∵抛物线y²=2px的焦点为（

p

2

，0），抛物线与双曲线

x2

a2

-

y2

b2

=1有相同的焦点F，
∴双曲线焦点是F（

p

2

，0），可得c=

p

2

∵点A是两曲线的一个交点，且AF⊥x轴，
∴可设点A（

p

2

，y₀），根据点A既在抛物线上又在双曲线上，
可得

y02=2p× p 2 ( p 2 )2 a2 - y02 b2 =1

，

p2

4a2

-

p2

b2

=1…（*）
∵c=

p

2

，得p=2c
∴代入（*）得：

4c2

4a2

-

4c2

b2

=1，
将c²=a²+b²代入，可得

b2

a2

-

4a2

b2

-4=0，解之得

b

a

=

2+2 2

∵双曲线

x2

a2

-

y2

b2

=1的渐近线方程为：y=±

b

a

x
∴双曲线的斜率大于

2

的渐近线l方程为y=

b

a

x=

2+2 2

x
所以l的斜率的值为k=

2+2 2

故答案为：{k|k=

2+2 2

}

点评：本题给出抛物线与双曲线有共同的焦点，并且它们的交点在x轴上的射影恰好是焦点F，求双曲线渐近线的斜率，着重考查了双曲线与抛物线的标准方程和简单性质，属于中档题．