题目内容

已知向量 $数学公式$ ， $数学公式$ ，函数 $数学公式$
（1）求f（x）的最小正周期；
（2）若0≤x≤π，求f（x）的最大值和最小值．

解：（1）向量 $\text{[math]}$ ， $\text{[math]}$ ，函数 $\text{[math]}$
∴ $\text{[math]}$
f（x）的最小正周期T=4π．
（2）∵0≤x≤π
∴ $\text{[math]}$ ，当 $\text{[math]}$ ，
即 $\text{[math]}$ 时，f（x）有最大值2；
当 $\text{[math]}$ ，
即x=π时，f（x）有最小值1．
分析：（1）根据所给的两个向量的坐标和函数的表示式，根据两个向量的数量积的坐标形式写出三角函数式，利用幅角公式写出最简形式，求出周期．
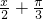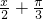（2）根据所给的x的范围写出 $\text{[math]}$ 的范围，根据正弦曲线的特点写出函数的最大值和最小值．
点评：本题考查三角函数的性质，是一个以向量为载体的题目，这种题目经常出现在高考卷中，是一个典型的三角函数解答题目．

练习册系列答案

阅读授之以渔系列答案

浙江省普通高中作业本系列答案

实验班中考总复习系列答案

亮点激活期末冲刺大试卷系列答案

全优学习达标训练系列答案

毕业会考阶梯模拟卷系列答案

小学升学多伦夯基总复习系列答案

同步练习目标与测试系列答案

复习计划风向标暑系列答案

开心快乐假期作业暑假作业西安出版社系列答案

相关题目

（本小题满分12分）已知向量,，设函数 , （1）求的最小正周期与单调递减区间。（2）在中，、、分别是角、、的对边，若,,的面积为，求的值。

已知向量，设函数＋1

（1）若， ,求的值；

（2）在△ABC中，角A，B，C的对边分别是，且满足，求的取值范围．

已知向量且，函数（1）求函数的最小正周期及单调递增区间；

（2）若，分别求及的值

（本小题10分）已知向量，定义函数

（1）求函数最小正周期；

（2）在△ABC中,角A为锐角，且，求边AC的长．

（本小题共10分）已知向量，，函数

（1）求的最小正周期；

（2）若，求的最大值和最小值