题目内容
已知正项等比数列{an},a1=2,又bn=log2an,且数列{bn}的前7项和T7最大,T7≠T6,且T7≠T8,则数列{an}的公比q的取值范围是( )(A)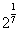 <q<
<q<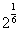 (B)
(B)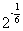 <q<
<q<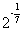 (C)q<
(C)q<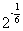 或q>
或q>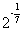 (D)q>
(D)q>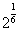 或q<
或q<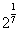
B.∵bn=log2an,而{a n}是以a1=2为首项,q为公比的等比数列,∴bn=log2an=log2(a1qn-1)=
n}是以a1=2为首项,q为公比的等比数列,∴bn=log2an=log2(a1qn-1)= 1+(n-1)log2q.
1+(n-1)log2q.
∴bn+1-bn=log2q.∴{bn}是等差数列,由于前7项之和T7最大,且T7≠T6,所以有 解得-
解得- <log2q<-
<log2q<- ,
,
即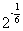 <q<
<q<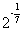 .故选B.
.故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设f(x)是定义在R上恒不为0的函数,对任意x,y∈R,都有f(x)•f(y)=f(x+y),若a1= ,an=f(n)(n为常数),则数列{an}的前n项和Sn的取值范围是( )
,an=f(n)(n为常数),则数列{an}的前n项和Sn的取值范围是( )
|
| A. | [ | B. | [ | C. | [ | D. | [ |
 ,则
,则 是锐角三角形”是真命题;
是锐角三角形”是真命题;  ,则
,则 ”的逆命题为真命题;③
”的逆命题为真命题;③  ;
;  的最小正周期是
的最小正周期是 ; ⑤ 在△ABC中,
; ⑤ 在△ABC中, 是
是 的充要条件; 其中错误的是 .
的充要条件; 其中错误的是 .  的前
的前 项和为
项和为 且满足
且满足 则
则 中最大的项为 ( )
中最大的项为 ( )







 ,把数列
,把数列 的各项排列成如下的三角形状,记
的各项排列成如下的三角形状,记 表示第
表示第 行的第
行的第 = ( ) A.
= ( ) A. B.
B. C.
C.  D.
D.

 。下列命题中真命题是 ( )
。下列命题中真命题是 ( ) n∈N*总有
n∈N*总有 ∥
∥ 成立,则数列{an}是等差数列 B.若
成立,则数列{an}是等差数列 B.若 中,
中,  ,数列
,数列 是等比数列,且
是等比数列,且 ,则
,则 ( ) A.4 B.8 C.16 D.36
( ) A.4 B.8 C.16 D.36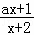 在区间(﹣2,+∞)上为增函数,则实数a的取值范围是 .
在区间(﹣2,+∞)上为增函数,则实数a的取值范围是 .