题目内容
已知等比数列{an}的前10项的积为32,则以下命题为真命题的是
- A.数列{an}的各项均为正数
- B.数列{an}中必有小于
 的项
的项 - C.数列{an}的公比必是正数
- D.数列{an}中的首项和公比中必有一个大于1
C
分析:由等比数列的性质可知 ,故q必是正数,故选项C为真命题;由
,故q必是正数,故选项C为真命题;由 可知a5可以为负数,故A为假命题;对于选项B,由于a5a6=2可以前10项全为
可知a5可以为负数,故A为假命题;对于选项B,由于a5a6=2可以前10项全为 ,故B为假命题;对于选项D,由
,故B为假命题;对于选项D,由 可得
可得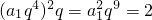 ,可取q=1、
,可取q=1、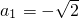 均不大于1,故D为假命题.
均不大于1,故D为假命题.
解答:由等比数列的性质,a1a2a3…a10=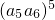 =32.
=32.
∴a5a6=2,设公比为q,则 ,故q必是正数,故选项C为真命题.
,故q必是正数,故选项C为真命题.
对于选项A,由 可知a5可以为负数,故A为假命题;
可知a5可以为负数,故A为假命题;
对于选项B,由a5a6=2可以前10项全为 ,故B为假命题;
,故B为假命题;
对于选项D,由 可得
可得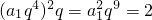 ,
,
可取q=1、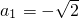 均不大于1,故D为假命题.
均不大于1,故D为假命题.
故选C.
点评:本题为命题真假的判断,由等比数列的性质得出 ,推出q必是正数是解决问题的关键,属基础题.
,推出q必是正数是解决问题的关键,属基础题.
分析:由等比数列的性质可知
 ,故q必是正数,故选项C为真命题;由
,故q必是正数,故选项C为真命题;由 可知a5可以为负数,故A为假命题;对于选项B,由于a5a6=2可以前10项全为
可知a5可以为负数,故A为假命题;对于选项B,由于a5a6=2可以前10项全为 ,故B为假命题;对于选项D,由
,故B为假命题;对于选项D,由 可得
可得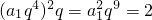 ,可取q=1、
,可取q=1、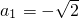 均不大于1,故D为假命题.
均不大于1,故D为假命题.解答:由等比数列的性质,a1a2a3…a10=
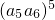 =32.
=32.∴a5a6=2,设公比为q,则
 ,故q必是正数,故选项C为真命题.
,故q必是正数,故选项C为真命题.对于选项A,由
 可知a5可以为负数,故A为假命题;
可知a5可以为负数,故A为假命题;对于选项B,由a5a6=2可以前10项全为
 ,故B为假命题;
,故B为假命题;对于选项D,由
 可得
可得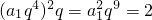 ,
,可取q=1、
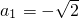 均不大于1,故D为假命题.
均不大于1,故D为假命题.故选C.
点评:本题为命题真假的判断,由等比数列的性质得出
 ,推出q必是正数是解决问题的关键,属基础题.
,推出q必是正数是解决问题的关键,属基础题. 
练习册系列答案
相关题目