题目内容
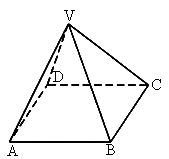
已知四棱锥
V-ABCD，如图，底面面积为16，一条侧棱长为
，计算它的高和斜高．
答案：略
解析：
解析：
|
解：设 VO为正四棱锥V-ABCD的高，作OM⊥BC于点M，则M为BC中点．连结OV，OB，则VO⊥OM，VO⊥OB．∵底面正方形 ABCD面积为16，∴ BC=4，BM=CM=2，
又∵  ，在Rt△VOB中，
由勾股定理可得  ．
在 Rt△VOM(或Rt△VBM)中，由勾股定理，得 ，或 ．
即正四棱锥的高为 6，斜高为 ． |
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
如图，已知在四棱锥P-ABCD中，底面ABCD是菱形，PA⊥底面ABCD，AB=1，PA•AC=1，∠ABC=θ（0＜θ＜
的体积为V．P，Q分别是侧棱A
，C
上的点，且AP＝
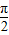），则四棱锥P-ABCD的体积V的取值范围是（ ）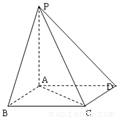
）
]
]
）
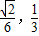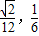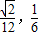V B、 
V C、 
V D、 
V