题目内容
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点,如果函数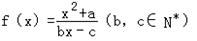 有且仅有两个不动点0,2,且
有且仅有两个不动点0,2,且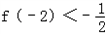 。
。
(1)求函数f(x)的单调区间;
(2)已知数列{an}各项不为零且不为1,满足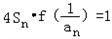 ,求证:
,求证: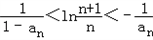 ;
;
(3)设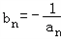 ,Tn为数列{bn}的前n项和,求证:T2012-1<ln2012<T2011。
,Tn为数列{bn}的前n项和,求证:T2012-1<ln2012<T2011。
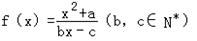 有且仅有两个不动点0,2,且
有且仅有两个不动点0,2,且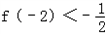 。
。(1)求函数f(x)的单调区间;
(2)已知数列{an}各项不为零且不为1,满足
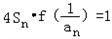 ,求证:
,求证: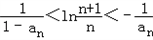 ;
;(3)设
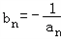 ,Tn为数列{bn}的前n项和,求证:T2012-1<ln2012<T2011。
,Tn为数列{bn}的前n项和,求证:T2012-1<ln2012<T2011。解:(1)设 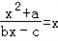 ,可得 (1-b)x2+cx+a=0,(b≠1)
,可得 (1-b)x2+cx+a=0,(b≠1)
由于函数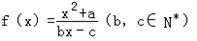 有且仅有两个不动点0,2,
有且仅有两个不动点0,2,
故0,2是方程(1-b)x2+cx+a=0的两个根,
∴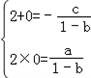 ,解得
,解得 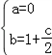 ,
,
所以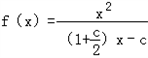
由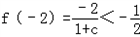
可得-1<c<3
又b,c∈N*,
所以c=2,b=2,
所以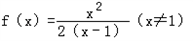 ,
,
于是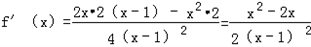 ,
,
令f′(x)>0,求得 x<0,或x>2,求得f(x)的增区间为(-∞,0),(2,+∞)
令f′(x)<0,求得 0<x<1,或2>x>1,
求得f(x)的增区间为(0,1),(1,2)。
(2)由已知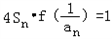 可得
可得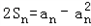 ,
,
当n≥2时,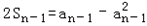
两式相减得(an+an-1)(an-an-1+1)=0,
所以an=-an-1或an-an-1=-1
当n=1时,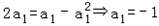 ,
,
若an=-an-1,则a2=1与an≠1矛盾,所以an-an-1=-1,
从而an=-n,
于是要证的不等式即为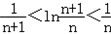 ,
,
于是我们可以考虑证明不等式: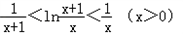 ,
,
令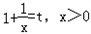 ,
,
则t>1,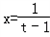
再令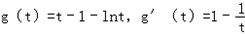 ,
,
由t∈(1,+∞)知g′(t)>0,
所以当t∈(1,+∞)时,g(t)单调递增,
所以g(t)>g(1)=0,
于是t-1>lnt,
即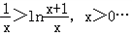 ①
①
令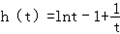 ,
,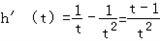 ,
,
当t∈(1,+∞)时,h(t)单调递增,
所以h(t)>h(1)=0,于是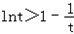 ,
,
即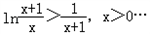
由①②可知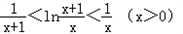 ,
,
所以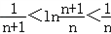 ,即原不等式成立。
,即原不等式成立。
(3)由(2)可知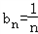 ,
,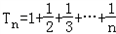 ,
,
在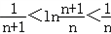 中,令n=1,2,3,4,…,2011,
中,令n=1,2,3,4,…,2011,
并将各式相加得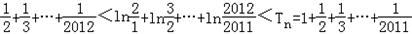 ,
,
即T2012-1<ln2012<T2011。
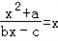 ,可得 (1-b)x2+cx+a=0,(b≠1)
,可得 (1-b)x2+cx+a=0,(b≠1)由于函数
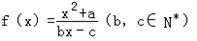 有且仅有两个不动点0,2,
有且仅有两个不动点0,2,故0,2是方程(1-b)x2+cx+a=0的两个根,
∴
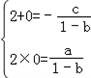 ,解得
,解得 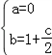 ,
,所以
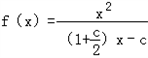
由
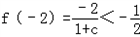
可得-1<c<3
又b,c∈N*,
所以c=2,b=2,
所以
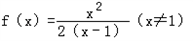 ,
,于是
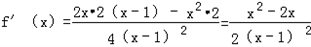 ,
,令f′(x)>0,求得 x<0,或x>2,求得f(x)的增区间为(-∞,0),(2,+∞)
令f′(x)<0,求得 0<x<1,或2>x>1,
求得f(x)的增区间为(0,1),(1,2)。
(2)由已知
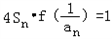 可得
可得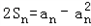 ,
,当n≥2时,
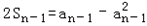
两式相减得(an+an-1)(an-an-1+1)=0,
所以an=-an-1或an-an-1=-1
当n=1时,
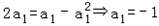 ,
,若an=-an-1,则a2=1与an≠1矛盾,所以an-an-1=-1,
从而an=-n,
于是要证的不等式即为
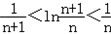 ,
,于是我们可以考虑证明不等式:
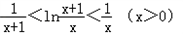 ,
,令
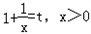 ,
,则t>1,
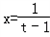
再令
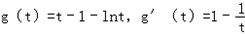 ,
,由t∈(1,+∞)知g′(t)>0,
所以当t∈(1,+∞)时,g(t)单调递增,
所以g(t)>g(1)=0,
于是t-1>lnt,
即
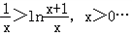 ①
①令
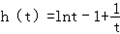 ,
,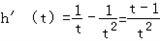 ,
,当t∈(1,+∞)时,h(t)单调递增,
所以h(t)>h(1)=0,于是
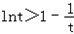 ,
,即
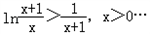
由①②可知
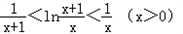 ,
,所以
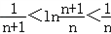 ,即原不等式成立。
,即原不等式成立。(3)由(2)可知
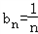 ,
,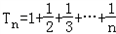 ,
,在
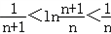 中,令n=1,2,3,4,…,2011,
中,令n=1,2,3,4,…,2011,并将各式相加得
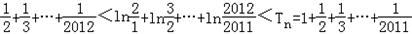 ,
,即T2012-1<ln2012<T2011。

练习册系列答案
相关题目