题目内容
已知函数f(x)=2sinxcosx+| 3 |
(1)将函数f(x)化为Asin(ωx+φ)(ω>0,|φ|<
| π |
| 2 |
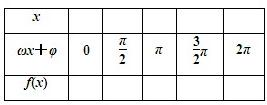
并画出函数f(x)在区间[-
| 1 |
| 6 |
| 5 |
| 6 |
(2)求函数f(x)的单调减区间.
分析:(1)用二倍角公式化简得f(x)=2sin(2x+
),根据五点法作图规则填表.用描点法作出图象.
(2)由三角函数的性质可以得到2kπ+
≤2x+
≤2kπ+
(k∈Z),解出x的范围既得函数f(x)的单调减区间.
| π |
| 3 |
(2)由三角函数的性质可以得到2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解答:解:(1)f(x)=2sinxcosx+
(2cos2x-1)
=sin2x+
cos2x=2sin(2x+
).
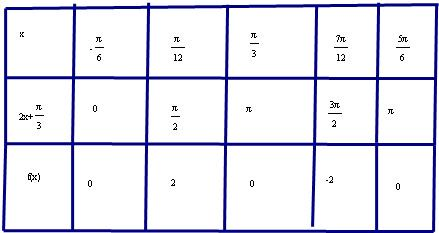

(2)由2kπ+
≤2x+
≤2kπ+
(k∈Z)得
kπ+
≤x≤kπ+
(k∈Z),
故函数f(x)的单调减区间为[kπ+
,kπ+
](k∈Z).
| 3 |
=sin2x+
| 3 |
| π |
| 3 |


(2)由2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
kπ+
| π |
| 12 |
| 7π |
| 12 |
故函数f(x)的单调减区间为[kπ+
| π |
| 12 |
| 7π |
| 12 |
点评:本题考点是五点法作正弦类函数的图象,此题是令相位取正弦函数五点法作图中的几个值,列出表格,描点作图.

练习册系列答案
相关题目