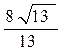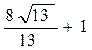题目内容
(本小题满分10分)已知圆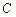 方程为:
方程为: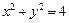 .
.
(1)直线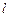 过点
过点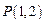 ,且与圆
,且与圆
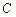 交于
交于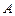 、
、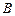 两点,若
两点,若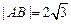 ,求直线
,求直线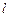 的方程;
的方程;
(2)过圆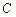 上一动点
上一动点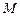 作平行于
作平行于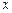 轴的直线
轴的直线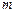 ,设
,设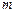 与
与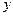 轴的交点为
轴的交点为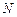 ,若向量
,若向量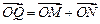 ,求动点
,求动点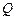 的轨迹方程。
的轨迹方程。
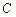 方程为:
方程为: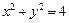 .
.(1)直线
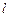 过点
过点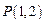 ,且与圆
,且与圆
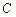 交于
交于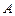 、
、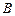 两点,若
两点,若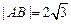 ,求直线
,求直线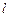 的方程;
的方程;(2)过圆
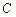 上一动点
上一动点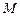 作平行于
作平行于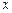 轴的直线
轴的直线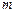 ,设
,设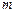 与
与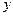 轴的交点为
轴的交点为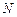 ,若向量
,若向量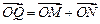 ,求动点
,求动点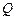 的轨迹方程。
的轨迹方程。(1),所求直线为 或
或
(2) 点的轨迹方程是
点的轨迹方程是 ,
,
 或
或
(2)
 点的轨迹方程是
点的轨迹方程是 ,
, (本小题10分)解:(1)①当直线 垂直于
垂直于 轴时,则此时直线方程为
轴时,则此时直线方程为 ,
, 与圆的两个交点坐标为
与圆的两个交点坐标为 和
和 ,其距离为
,其距离为 满足题意 ………1分
满足题意 ………1分
②若直线 不垂直于
不垂直于 轴,设其方程为
轴,设其方程为 ,即
,即
设圆心到此直线的距离为 ,则
,则 ,得
,得 …………3分
…………3分
∴ ,
, ,
, 
故所求直线方程为 ……………………4分
……………………4分
综上所述,所求直线为 或
或 ………5分
………5分
(2)设点 的坐标为
的坐标为 (
( ),
),
 点坐标为
点坐标为
则 点坐标是
点坐标是 ………………6分
………………6分
∵ ,∴
,∴ 即
即 ,
,
 ……7分
……7分
又∵ ,∴
,∴ ………………8分
………………8分
∴ 点的轨迹方程是
点的轨迹方程是 , ………… 10分
, ………… 10分
 垂直于
垂直于 轴时,则此时直线方程为
轴时,则此时直线方程为 ,
, 与圆的两个交点坐标为
与圆的两个交点坐标为 和
和 ,其距离为
,其距离为 满足题意 ………1分
满足题意 ………1分②若直线
 不垂直于
不垂直于 轴,设其方程为
轴,设其方程为 ,即
,即
设圆心到此直线的距离为
 ,则
,则 ,得
,得 …………3分
…………3分 ∴
 ,
, ,
, 
故所求直线方程为
 ……………………4分
……………………4分 综上所述,所求直线为
 或
或 ………5分
………5分 (2)设点
 的坐标为
的坐标为 (
( ),
),
 点坐标为
点坐标为
则
 点坐标是
点坐标是 ………………6分
………………6分 ∵
 ,∴
,∴ 即
即 ,
,
 ……7分
……7分又∵
 ,∴
,∴ ………………8分
………………8分∴
 点的轨迹方程是
点的轨迹方程是 , ………… 10分
, ………… 10分
练习册系列答案
相关题目
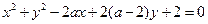 ,其中
,其中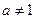 ,且
,且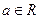 .
. 关于直线
关于直线 的对称圆的方程。
的对称圆的方程。 是
是 的切线,切点为
的切线,切点为 ,
, ,
, 是
是 交
交 ,
, ,则
,则



 的取值范围;
的取值范围; ON(O为坐标原点)求m的值;
ON(O为坐标原点)求m的值;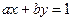 与圆
与圆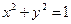 相交于
相交于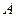 、
、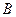 两点(其中
两点(其中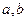 是实数),且
是实数),且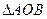 是直角三角形
是直角三角形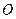 是坐标原点),则点
是坐标原点),则点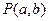 与点
与点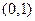 之间距离的最大值为 ▲ ;
之间距离的最大值为 ▲ ; 交于A、B两点,且
交于A、B两点,且 ,其中O为原点,则实数
,其中O为原点,则实数 的值为
的值为 或
或
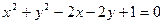 上的点到直线
上的点到直线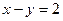 的距离的最大值是__________________
的距离的最大值是__________________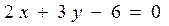 上运动,另一点B在圆
上运动,另一点B在圆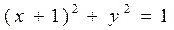 上运动,则|AB|的最小值是
上运动,则|AB|的最小值是