Question

判断下列函数的奇偶性:

（1）)；（2）f(x)=sin(cosx);

（3）；（4）.

Answer 1

思路分析:先求函数的定义域，再利用奇函数或偶函数的定义判断函数的奇偶性.

解：（1）函数的定义域为R，且f(x)=cos(x+)=-sinx.

由于f(-x)=-sin(-x)=sinx=-f(x).

所以函数为奇函数.

（2）函数的定义域为R，且由于f(-x)=sin(cos(-x))=sin(cosx)=f(x).

所以函数f(x)=sin(cosx)为偶函数.

（3）由，解得-1＜x≤1，则函数的定义域不关于原点对称，

所以函数 既不是奇函数也不是偶函数.

（4）由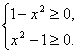得x=±1，即函数的定义域为{-1，1}.

又.

所以f(-x)=0=-f(x)=f(x).

所以函数既是奇函数又是偶函数.

方法归纳 在判断函数的奇偶性时应首先求出函数的定义域，然后将其解析式化为最简解析式后再利用定义来判断.

误区警示 在判断函数的奇偶性时，容易忽略对函数解析式的化简，从而导致结论错误.