题目内容
在△ABC中,a,b,c分别是三内角A,B,C的对边,S为△ABC的面积.若向量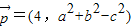 ,
,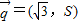 满足
满足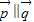 ,则∠C=( )
,则∠C=( )A.
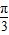
B.
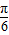
C.
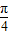
D.
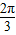
【答案】分析:由向量的平行可得4S=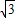 (a2+b2-c2),由三角形的面积公式和余弦定理代入上式化简可得sinC=
(a2+b2-c2),由三角形的面积公式和余弦定理代入上式化简可得sinC=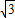 cosC,进而可得tanC=
cosC,进而可得tanC=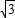 ,即可得答案.
,即可得答案.
解答:解:∵向量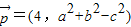 ,
,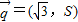 满足
满足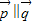 ,
,
∴4S=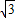 (a2+b2-c2),
(a2+b2-c2),
而由余弦定理可得:a2+b2-c2=2abcosC,又S= absinC,
absinC,
代入上式4S=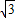 (a2+b2-c2)可得2absinC=2
(a2+b2-c2)可得2absinC=2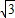 abcosC,即sinC=
abcosC,即sinC=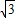 cosC,
cosC,
由同角三角函数的基本关系可得:tanC=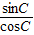 =
=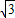 ,
,
故∠C=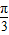 .
.
故选A
点评:本题考查向量平行的充要条件,熟练掌握三角形的面积公式和余弦定理是解决问题的关键,属基础题.
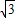 (a2+b2-c2),由三角形的面积公式和余弦定理代入上式化简可得sinC=
(a2+b2-c2),由三角形的面积公式和余弦定理代入上式化简可得sinC=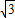 cosC,进而可得tanC=
cosC,进而可得tanC=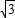 ,即可得答案.
,即可得答案.解答:解:∵向量
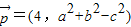 ,
,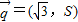 满足
满足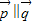 ,
,∴4S=
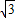 (a2+b2-c2),
(a2+b2-c2),而由余弦定理可得:a2+b2-c2=2abcosC,又S=
 absinC,
absinC,代入上式4S=
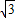 (a2+b2-c2)可得2absinC=2
(a2+b2-c2)可得2absinC=2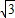 abcosC,即sinC=
abcosC,即sinC=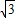 cosC,
cosC,由同角三角函数的基本关系可得:tanC=
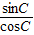 =
=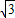 ,
,故∠C=
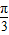 .
.故选A
点评:本题考查向量平行的充要条件,熟练掌握三角形的面积公式和余弦定理是解决问题的关键,属基础题.

练习册系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|