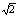题目内容
 如图,位于A地正北方向的Z地某日某时发生地震,A地于当日13时46分01秒测得地震信号,位于A地正东方向34.64km处的B地于当日13时46分06秒测得地震信号,试求位于B地北偏东60°方向24km远处的C地大约什么时间测得地震信号?
如图,位于A地正北方向的Z地某日某时发生地震,A地于当日13时46分01秒测得地震信号,位于A地正东方向34.64km处的B地于当日13时46分06秒测得地震信号,试求位于B地北偏东60°方向24km远处的C地大约什么时间测得地震信号?
( ,地震波传播速度为4km/s)
,地震波传播速度为4km/s)
解:连接ZC,设地震波从Z地到A地所需时间为t秒,则ZA=4t(km),ZB=4(t+5)(km),
在Rt△ZAB中,由勾股定理得16(t+5)2=16t2+34.642,t=4.99956≈5,
∴地震发生时间为13时45分56秒,
∴ZB=40,ZA=20,∴tan∠AZB= =
= =1.732=
=1.732= ,∴∠AZB=60°,∴∠ZBC=120°,
,∴∠AZB=60°,∴∠ZBC=120°,
在△ZBC中,由余弦定理得:ZC2=402+242-2×40×24×cos120°=562
∴ZC=56,∴地震波从Z地到C地所需时间为 =14,
=14,
∴C地大约13时46分10秒测得地震信号.
分析:设地震波从Z地到A地所需时间为t秒,在Rt△ZAB中,由勾股定理得t≈5,得地震发生时间,得ZB,ZA的长度,及tan∠AZB,求出∠AZB的度数,可得∠ZBC的度数,在△ZBC中,由余弦定理得ZC的长度,由长度除以速度可得从Z地到C地所需时间,在地震发生时间的基础上加上这个时间可得结果.
点评:本题考查解三角形的实际应用,主要问题是如何把实际问题转化为数问题,画图,清晰直观,有利于分析、解决问题.
在Rt△ZAB中,由勾股定理得16(t+5)2=16t2+34.642,t=4.99956≈5,
∴地震发生时间为13时45分56秒,
∴ZB=40,ZA=20,∴tan∠AZB=
 =
= =1.732=
=1.732= ,∴∠AZB=60°,∴∠ZBC=120°,
,∴∠AZB=60°,∴∠ZBC=120°,在△ZBC中,由余弦定理得:ZC2=402+242-2×40×24×cos120°=562
∴ZC=56,∴地震波从Z地到C地所需时间为
 =14,
=14,∴C地大约13时46分10秒测得地震信号.
分析:设地震波从Z地到A地所需时间为t秒,在Rt△ZAB中,由勾股定理得t≈5,得地震发生时间,得ZB,ZA的长度,及tan∠AZB,求出∠AZB的度数,可得∠ZBC的度数,在△ZBC中,由余弦定理得ZC的长度,由长度除以速度可得从Z地到C地所需时间,在地震发生时间的基础上加上这个时间可得结果.
点评:本题考查解三角形的实际应用,主要问题是如何把实际问题转化为数问题,画图,清晰直观,有利于分析、解决问题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
[番茄花园1] 为了能更好地了解鲸的生活习性,某动物研究所在受伤的鲸身上安装了电子监测装置,从海岸放归点A处(如图所示)把它放归大海,并沿海岸线由西到东不停地对鲸进行了40分钟的跟踪观测,每隔10分钟踩点测得数据如下表(设鲸沿海面游动)。然后又在观测站B处对鲸进行生活习性的详细观测。已知AB=15km,观测站B的观测半径为5km.

观测时刻t (分钟) |
跟踪观测点到放归点距离a(km) |
鲸位于跟踪观测点正北方向的距离b(km) |
|
10 |
1 |
1 |
|
20 |
2 |
|
|
30 |
3 |
|
|
40 |
4 |
2 |
(I)根据表中数据:(1)计算鲸沿海岸线方向运动的速度,(2)写出a、b满足的关系式,并画出鲸的运动路线简图;
(II)若鲸继续以(I)-(2)中的运行路线运动,则鲸经过多少分钟(从放归时计时),可进入前方观测站B的观测范围。()
[番茄花园1]18.
 A,B为两地震监测站,B在A的正东方向,且相距100千米,C在A南偏东30°的方向上,(如图)C处发生地震时(C处为地震中心),A监测站比B监测站早2秒钟监测到,已知地震波的传播速度为2千米/秒.
A,B为两地震监测站,B在A的正东方向,且相距100千米,C在A南偏东30°的方向上,(如图)C处发生地震时(C处为地震中心),A监测站比B监测站早2秒钟监测到,已知地震波的传播速度为2千米/秒. 如图,位于A地正北方向的Z地某日某时发生地震,A地于当日13时46分01秒测得地震信号,位于A地正东方向34.64km处的B地于当日13时46分06秒测得地震信号,试求位于B地北偏东60°方向24km远处的C地大约什么时间测得地震信号?
如图,位于A地正北方向的Z地某日某时发生地震,A地于当日13时46分01秒测得地震信号,位于A地正东方向34.64km处的B地于当日13时46分06秒测得地震信号,试求位于B地北偏东60°方向24km远处的C地大约什么时间测得地震信号?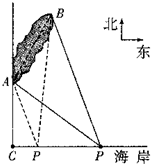 如图,在一条东西方向的海岸线上的点C处有一个原子能研究所,海岸线北侧有一个小岛,岛上建有一个核电站,该岛的一个端点A位于点C的正北方向4
如图,在一条东西方向的海岸线上的点C处有一个原子能研究所,海岸线北侧有一个小岛,岛上建有一个核电站,该岛的一个端点A位于点C的正北方向4