题目内容
已知某圆的方程是x2+y2=4,A、B为圆上两动点,M(1,1)为圆内一定点,若四边形MAPB为矩形,求P点的轨迹方程.
解:设P点坐标为(x,y),A、B两点的坐标分别为(x1,y1)、(x2,y2).
∵四边形MAPB为矩形,∴AB的中点与MP的中点重合,且MA⊥MB.
于是得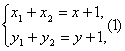
且![]() =-1. (2)
=-1. (2)
将(2)式整理,得
x1x2+y1y2+2=(x1+x2)+(y1+y2). (3)
将(1)式代入(3)式得x1x2+y1y2=x+y. (4)
∵A、B在圆上,
∴x12+y12=4,x22+y22=4.
∴x12+y12+x22+y22=8,
即(x1+x2)2+(y1+y2)2-2(x1x2+y1y2)=8.
将(1)(4)式代入上式得(x+1)2+(y+1)2-2(x+y)=8,
化简得x2+y2=6,这就是P点的轨迹方程.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
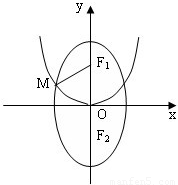
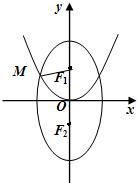 与向量、圆交汇.例5:已知F1、F2分别为椭圆C1:
与向量、圆交汇.例5:已知F1、F2分别为椭圆C1: 如图,已知F1、F2分别为椭圆
如图,已知F1、F2分别为椭圆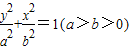 的上、下焦点,其中F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且
的上、下焦点,其中F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且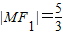 .
.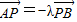 ,
,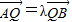 ,(λ≠0且λ≠±1).问点Q是否总在某一定直线上?若在,求出这条直线,否则,说明理由.
,(λ≠0且λ≠±1).问点Q是否总在某一定直线上?若在,求出这条直线,否则,说明理由.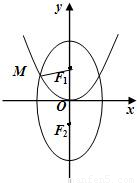
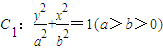 的上、下焦点,其中F1也是抛物线
的上、下焦点,其中F1也是抛物线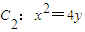 的焦点,点M是C1与C2在第二象限的交点,且
的焦点,点M是C1与C2在第二象限的交点,且 .
.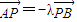 ,
,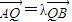 (λ≠0且λ≠±1),
(λ≠0且λ≠±1),