Question

函数f（x）=x³-x²+x+1在点（1，2）处的切线与函数g（x）=x²围成的图形的面积等于________．

Answer 1

分析：由题意利用导数可求得过点（1，2）处的切线方程，利用定积分即可求得切线与函数g（x）=x²围成的图形的面积．
解答：解：∵（1，2）为曲线f（x）=x³-x²+x+1上的点，设过点（1，2）处的切线的斜率为k，
则k=f′（1）=（3x²-2x+1）|_x=1=2，
∴过点（1，2）处的切线方程为：y-2=2（x-1），即y=2x．
∴y=2x与函数g（x）=x²围成的图形如图：
由得二曲线交点A（2，4），
又S_△AOB=×2×4=4，g（x）=x²围与直线x=2，x轴围成的区域的面积S=x²dx==，
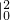∴y=2x与函数g（x）=x²围成的图形的面积为：S′=S_△AOB-S=4-=．
故答案为：．
点评：本题考查导数的几何意义，考查定积分在求面积中的应用，求得题意中过点（1，2）处的切线方程是关键，考查作图与运算能力，属于中档题．