已知函数f(x)=x3+ax2+bx+2a在x=1处有极值为10.求a.b的值及f(x)的极值. 题目和参考答案——青夏教育精英家教网—

题目内容

已知函数f(x)=x³+ax²+bx+2a在x=1处有极值为10，求a、b的值及f(x)的极值.

解：f′(x)=3x²+2ax+b,∵f(x)在x=1处有极值10,

∴

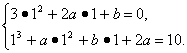
解得

∴f(x)=x³+12x²-27x+24.

f′(x)=3(x+9)(x-1).

令f′(x)=0,解得x₁=-9,x₂=1.当x变化时，f′(x),f(x)的变化情况如下表：

x	(-∞,-9)	-9	(-9,1)	1	(1,+∞)
f′(x)	+	0	-	0	+
f(x)	↗	极大值510	↘	极小值10	↗

因此，当x=-9时，y有极大值，并且,y_极大值=510;

当x=1时，y有极小值，并且,y_极小值=10.

练习册系列答案

（2011•上海模拟）已知函数f(x)=(

-1)2+(

-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2^m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k²，b=（k+c）²时，记f（x）=f₁（x）；当a=（k+c）²，b=（k+2c）²时，记f（x）=f₂（x）．
求证：f1(x)+f2(x)＞

4c2

k(k+c)

．

已知函数f(x)的图像在[a，b]上连续不断，f₁(x)＝min{f(t)|a≤t≤x}(x∈[a，b])，f₂(x)＝max{f(t)|a≤t≤x}(x∈[a，b])，其中，min{f(x)|x∈D}表示函数f(x)在D上的最小值，max{f(x)|x∈D}表示函数f(x)在D上的最大值，若存在最小正整数k，使得f₂(x)－f₁(x)≤k(x－a)对任意的x∈[a，b]成立，则称函数f(x)为[a，b]上的“k阶收缩函数”．已知函数f(x)＝x²，x∈[－1，4]为[－1，4]上的“k阶收缩函数”，则k的值是_________．

已知函数f（x）、g（x），下列说法正确的是（）
A．f（x）是奇函数，g（x）是奇函数，则f（x）+g（x）是奇函数
B．f（x）是偶函数，g（x）是偶函数，则f（x）+g（x）是偶函数
C．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）一定是奇函数或偶函数
D．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）可以是奇函数或偶函数

试题分类