Question

函数f（x）=x²+|x+a|-b的图象上存在点P（x₁，f（x₁））对任意a∈[-1，3]都不在x轴的上方，则b的最小值为________．

Answer 1

分析：由函数f（x）=x²+|x+a|-b的图象上存在点P（x₁，f（x₁））对任意a∈[-1，3]都不在x轴的上方，可得任意a∈[-1，3]，函数f（x）的最小值f（x）_min≤0恒成立，分a∈[-1，-]时，a∈（-，）时和a∈[，3]时三种情况，讨论（x）_min≤0恒成立时b的范围，最后综合分类结果，即可得到答案．
解答：若函数f（x）=x²+|x+a|-b的图象上对任意a∈[-1，3]
都有点P（x₁，f（x₁））都不在x轴的上方
则对任意a∈[-1，3]，函数f（x）的最小值f（x）_min≤0恒成立，
∵f（x）=
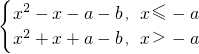
∵a∈[-1，3]
∴当a∈[-1，-]时，-a∈[，1]，此时f（x）_min=f（）=--a-b，
若f（x）_min≤0恒成立，则b≥
∴当a∈（-，）时，-a∈（-，），此时f（x）_min=f（-a）=a²-b，
若f（x）_min≤0恒成立，则b≥1
当a∈[，3]时，-a∈[-3，-]，此时f（x）_min=f（-）=-+a-b，
若f（x）_min≤0恒成立，则b≥
若f（x）_min≤0恒成立，则b的最小值为
故答案为
点评：本题考查的知识点是二次函数的性质，二次函数的图象，其中分类讨论出a∈[-1，-]时，a∈（-，）时和a∈[，3]时三种情况，讨论（x）_min≤0恒成立时b的范围，是解答本题的关键．