题目内容
在△ABC中,A,C为锐角,角A,B,C所对应的边分别为a,b,c,且cos2A=
,sinC=
.
(1)求cos(A+C)的值;
(2)若a-c=
-1,求a,b,c的值;
(3)已知tan(α+A+C)=2,求
的值.
| 3 |
| 5 |
| ||
| 10 |
(1)求cos(A+C)的值;
(2)若a-c=
| 2 |
(3)已知tan(α+A+C)=2,求
| 1 |
| 2sinαcosα+cos2α |
(1)∵cos2A=2cos2A-1=
,且A为锐角
∴cosA=
,sinA=
=
∵sinC=
,且C为锐角
∴cosC=
=
因此,cos(A+C)=cosAcosC-sinAsinC=
•
-
•
=
(2)∵cos(A+C)=
,0<A+C<π,∴A+C=
,得B=π-
=
,sinB=
∵sinA=
,sinB=
,sinC=
,
∴sinA:sinB:sinC=2
:5
:
由正弦定理,得a:b:c=2
:5
:
,设a=2
x,得b=5
x,c=
x
∵a-c=
-1,得2
x-
x=
-1
∴x=
,可得a=
,b=
,c=1
(3)由(2)知A+C=
,得tan(α+
)=2
∴
=2,解之得tanα=
所以
=
=
=
| 3 |
| 5 |
∴cosA=
2
| ||
| 5 |
| 1-cos2A |
| ||
| 5 |
∵sinC=
| ||
| 10 |
∴cosC=
| 1-sin2C |
3
| ||
| 10 |
因此,cos(A+C)=cosAcosC-sinAsinC=
2
| ||
| 5 |
3
| ||
| 10 |
| ||
| 5 |
| ||
| 10 |
| ||
| 2 |
(2)∵cos(A+C)=
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
∵sinA=
| ||
| 5 |
| ||
| 2 |
| ||
| 10 |
∴sinA:sinB:sinC=2
| 5 |
| 2 |
| 10 |
由正弦定理,得a:b:c=2
| 5 |
| 2 |
| 10 |
| 5 |
| 2 |
| 10 |
∵a-c=
| 2 |
| 5 |
| 10 |
| 2 |
∴x=
| ||
| 10 |
| 2 |
| 5 |
(3)由(2)知A+C=
| π |
| 4 |
| π |
| 4 |
∴
tanα+tan
| ||
1-tanαtan
|
| 1 |
| 3 |
所以
| 1 |
| 2sinαcosα+cos2α |
| cos2α+sin2α |
| 2sinαcosα+cos2α |
| 1+tan2α |
| 2tanα+1 |
| 2 |
| 3 |

练习册系列答案
相关题目
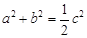 .则直线
.则直线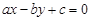 被圆
被圆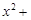
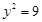 所截得的弦长为 .
所截得的弦长为 .