题目内容
已知函数f(x)=ax2+1,g(x)=x3+bx,其中a>0,b>0.
(Ⅰ)若曲线y=f(x)与曲线y=g(x)在它们的交点P(2,c)处有相同的切线(P为切点),求a,b的值;
(Ⅱ)令h(x)=f(x)+g(x),若函数h(x)的单调递减区间为[ ],求:
],求:
(1)函数h(x)在区间(一∞,-1]上的最大值M(a);
(2)若|h(x)|≤3,在x∈[-2,0]上恒成立,求a的取值范围.
解:(I)f(x)=ax2+1(a>0),则f'(x)=2ax,k1=4a,g(x)=x3+bx,则f'(x)=3x2+b,k2=12+b,
由(2,c)为公共切点,可得:4a=12+b ①
又f(2)=4a+1,g(2)=8+2b,
∴4a+1=8+2b,与①联立可得:a= ,b=5.
,b=5.
(Ⅱ)(1)由h(x)=f(x)+g(x)=x3+ax2+bx+1,
则h′(x)=3x2+2ax+b,
因函数h(x)的单调递减区间为[ ],∴当x∈[
],∴当x∈[ ]时,3x2+2ax+b≤0恒成立,
]时,3x2+2ax+b≤0恒成立,
此时,x=- 是方程3x2+2ax+b=0的一个根,得3(-
是方程3x2+2ax+b=0的一个根,得3(- )2+2a(-
)2+2a(- )+b=0,得a2=4b,
)+b=0,得a2=4b,
∴h(x)=x3+ax2+ a2x+1
a2x+1
令h'(x)=0,解得:x1=- ,x2=-
,x2=- ;
;
∵a>0,∴- <-
<- ,列表如下:
,列表如下:
| x | (-∞,- ) ) | - | (- ,- ,- ) ) | - | (- ,+∞ ,+∞ |
| h′(x) | + | ? | - | ? | + |
| h(x) | ? | 极大值 | ? | 极小值 | ? |
∴原函数在(-∞,- )单调递增,在(-
)单调递增,在(- ,-
,- )单调递减,在(-
)单调递减,在(- ,+∞)上单调递增
,+∞)上单调递增
①若-1≤- ,即a≤2时,最大值为h(-1)=a-
,即a≤2时,最大值为h(-1)=a- ;
;
②若- <-1<-
<-1<- ,即2<a<6时,最大值为h(-
,即2<a<6时,最大值为h(- )=1
)=1
③若-1≥- 时,即a≥6时,最大值为h(-
时,即a≥6时,最大值为h(- )=1.
)=1.
综上所述:当a∈(0,2]时,最大值为h(-1)=a- ;当a∈(2,+∞)时,最大值为h(-
;当a∈(2,+∞)时,最大值为h(- )=1.
)=1.
(2)由(1)知,函数h(x)在(-∞,- )单调递增,在(-
)单调递增,在(- ,-
,- )单调递减,在(-
)单调递减,在(- ,+∞)上单调递增
,+∞)上单调递增
故h(- )为极大值,h(-
)为极大值,h(- )=1;h(-
)=1;h(- )为极小值,h(-
)为极小值,h(- )=-
)=- ;
;
∵|h(x)|≤3,在x∈[-2,0]上恒成立,又h(0)=1.
∴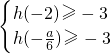 即
即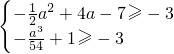 ,解得
,解得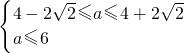
∴a的取值范围:4-2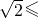 a≤6.
a≤6.
分析:(I)根据曲线y=f(x)与曲线y=g(x)在它们的交点(2,c)处具有公共切线,可知切点处的函数值相等,切点处的斜率相等,故可求a、b的值;
(II)(1)根据函数h(x)的单调递减区间为[
 ]得出a2=4b,构建函数h(x)=f(x)+g(x)=x3+ax2+
]得出a2=4b,构建函数h(x)=f(x)+g(x)=x3+ax2+ a2x+1,求导函数,利用导数的正负,可确定函数的单调区间,进而分类讨论,确定函数在区间(-∞,-1)上的最大值.
a2x+1,求导函数,利用导数的正负,可确定函数的单调区间,进而分类讨论,确定函数在区间(-∞,-1)上的最大值.(2)由(1)知,函数h(x)在(-∞,-
 )单调递增,在(-
)单调递增,在(- ,-
,- )单调递减,在(-
)单调递减,在(- ,+∞)上单调递增
,+∞)上单调递增,从而得出其极大值、极小值,再根据|h(x)|≤3,在x∈[-2,0]上恒成立,建立关于a的不等关系,解得a的取值范围即可.
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,解题的关键是正确求出导函数和应用分类讨论的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目