题目内容
定义在(-1,1)上的奇函数f(x)是减函数,且f(1-a)+f(1-a2)<0,求实数a的取值范围.
【答案】分析:先根据奇函数将f(1-a)+f(1-a2)<0化简一下,再根据f(x)是定义在(-1,1)上的减函数,建立不等式组进行求解即可.
解答:解:∵f(x)是奇函数
∴f(1-a)<-f(1-a2)=f(a2-1)
∵f(x)是定义在(-1,1)上的减函数
∴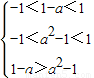 解得:0<a<1
解得:0<a<1
∴0<a<1.
点评:本题主要考查了函数单调性的应用,以及函数的奇偶性的应用,属于中档题.
解答:解:∵f(x)是奇函数
∴f(1-a)<-f(1-a2)=f(a2-1)
∵f(x)是定义在(-1,1)上的减函数
∴
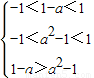 解得:0<a<1
解得:0<a<1∴0<a<1.
点评:本题主要考查了函数单调性的应用,以及函数的奇偶性的应用,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.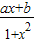 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.