题目内容
已知函数f(x)=2x2+ax-1,g(log2x)=x2-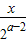 .
.(1)求函数g(x)的解析式,并写出当a=1时,不等式g(x)<8的解集;
(2)若f(x)、g(x)同时满足下列两个条件:①?t∈[1,4]使f(-t2-3)=f(4t) ②?x∈(-∞,a],g(x)<8.
求实数a的取值范围.
【答案】分析:(1)令t=log2t,则x=2t,故g(x)=(2x)2-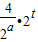 .由此能求出当a=1时,不等式g(x)<8的解集.
.由此能求出当a=1时,不等式g(x)<8的解集.
(2)①由-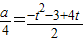 ,知a=2(t2-4t+3)=2(t-2)2-2,由t∈[1,4],得a∈[-2,6].②由
,知a=2(t2-4t+3)=2(t-2)2-2,由t∈[1,4],得a∈[-2,6].②由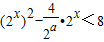 在x∈(-∞,a]上恒成立,知
在x∈(-∞,a]上恒成立,知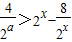 在x∈(-∞,a]上恒成立.综合①②,能求出符合条件的实数a的取值范围.
在x∈(-∞,a]上恒成立.综合①②,能求出符合条件的实数a的取值范围.
解答:解:(1)令t=log2t,则x=2t,
∴g(t)=(2t)2-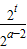 =(2t)2-
=(2t)2-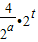 ,即g(x)=(2x)2-
,即g(x)=(2x)2-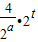 .
.
当a=1时,不等式g(x)<8,即(2x)2-2•2x-8<0.
∴2x<4,解得x<2.
∴不等式g(x)<8的解集是{x|x<2}.
(2)①由题意,-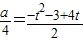 ,即a=2(t2-4t+3)=2(t-2)2-2,
,即a=2(t2-4t+3)=2(t-2)2-2,
由t∈[1,4],得a∈[-2,6].
②由题意,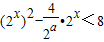 在x∈(-∞,a]上恒成立.
在x∈(-∞,a]上恒成立.
即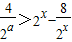 在x∈(-∞,a]上恒成立.
在x∈(-∞,a]上恒成立.
令μ=2x,则μ∈(0,2a],∴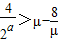 .
.
∵函数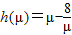 在(0,2a]上为增函数,
在(0,2a]上为增函数,
∴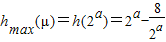 ,
,
∴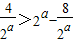 ,解得
,解得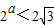 ,
,
∴a<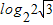 .
.
综合①②,符合条件的实数a的取值范围是{a|-2≤a<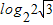 }.
}.
点评:本题考查不等式的解法和实数的取值范围的求法.解题时要认真审题,仔细解答,注意合理地进行等价转化.
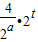 .由此能求出当a=1时,不等式g(x)<8的解集.
.由此能求出当a=1时,不等式g(x)<8的解集.(2)①由-
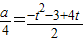 ,知a=2(t2-4t+3)=2(t-2)2-2,由t∈[1,4],得a∈[-2,6].②由
,知a=2(t2-4t+3)=2(t-2)2-2,由t∈[1,4],得a∈[-2,6].②由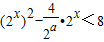 在x∈(-∞,a]上恒成立,知
在x∈(-∞,a]上恒成立,知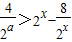 在x∈(-∞,a]上恒成立.综合①②,能求出符合条件的实数a的取值范围.
在x∈(-∞,a]上恒成立.综合①②,能求出符合条件的实数a的取值范围.解答:解:(1)令t=log2t,则x=2t,
∴g(t)=(2t)2-
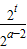 =(2t)2-
=(2t)2-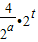 ,即g(x)=(2x)2-
,即g(x)=(2x)2-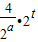 .
.当a=1时,不等式g(x)<8,即(2x)2-2•2x-8<0.
∴2x<4,解得x<2.
∴不等式g(x)<8的解集是{x|x<2}.
(2)①由题意,-
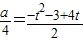 ,即a=2(t2-4t+3)=2(t-2)2-2,
,即a=2(t2-4t+3)=2(t-2)2-2,由t∈[1,4],得a∈[-2,6].
②由题意,
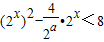 在x∈(-∞,a]上恒成立.
在x∈(-∞,a]上恒成立.即
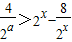 在x∈(-∞,a]上恒成立.
在x∈(-∞,a]上恒成立.令μ=2x,则μ∈(0,2a],∴
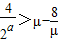 .
.∵函数
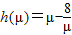 在(0,2a]上为增函数,
在(0,2a]上为增函数,∴
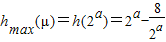 ,
,∴
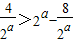 ,解得
,解得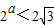 ,
,∴a<
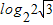 .
.综合①②,符合条件的实数a的取值范围是{a|-2≤a<
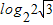 }.
}.点评:本题考查不等式的解法和实数的取值范围的求法.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目