题目内容
光线沿直线l1:x-2y+5=0射入,遇直线l:3x-2y+7=0后反射,求反射光线所在的直线方程.
29x-2y+33=0
方法一 由
得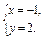
 ∴反射点M的坐标为(-1,2).
∴反射点M的坐标为(-1,2).
又取直线x-2y+5=0上一点P(-5,0),设P关于直线l的对称点 ,由P
,由P ⊥l可知,
⊥l可知,
kPP′=-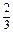 =
= .
.
而PP′的中点Q的坐标为 ,
,
Q点在l上,∴3·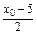 -2·
-2· +7=0.
+7=0.
由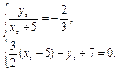 得
得
根据直线的两点式方程可得l的方程为29x-2y+33=0.
方法二 设直线x-2y+5=0上任意一点P(x0,y0)关于直线l的对称点为P′(x,y),
则 ,
,
又PP′的中点Q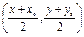 在l上,
在l上,
∴3×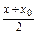 -2×
-2×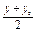 +7=0,
+7=0,
由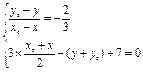
可得P点的坐标为
x0=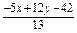 ,y0=
,y0=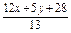 ,
,
代入方程x-2y+5=0中,
化简得29x-2y+33=0,即为所求反射光线所在的直线方程.

得
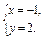
 ∴反射点M的坐标为(-1,2).
∴反射点M的坐标为(-1,2).又取直线x-2y+5=0上一点P(-5,0),设P关于直线l的对称点
 ,由P
,由P ⊥l可知,
⊥l可知,kPP′=-
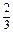 =
= .
.而PP′的中点Q的坐标为
 ,
,Q点在l上,∴3·
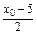 -2·
-2· +7=0.
+7=0.由
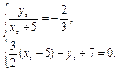 得
得
根据直线的两点式方程可得l的方程为29x-2y+33=0.
方法二 设直线x-2y+5=0上任意一点P(x0,y0)关于直线l的对称点为P′(x,y),
则
 ,
,又PP′的中点Q
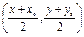 在l上,
在l上,∴3×
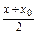 -2×
-2×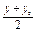 +7=0,
+7=0,由
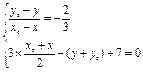
可得P点的坐标为
x0=
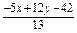 ,y0=
,y0=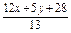 ,
,代入方程x-2y+5=0中,
化简得29x-2y+33=0,即为所求反射光线所在的直线方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

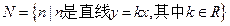 ,则集合
,则集合 的关系是( ).
的关系是( ).
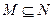

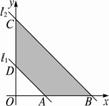
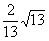
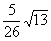
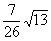
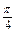 的直线方程.
的直线方程.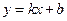 中,当
中,当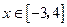 时,
时,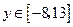 ,求此直线的方程.
,求此直线的方程.