题目内容

如图所示，直三棱柱ABC-A1B1C1中，已知∠ABC=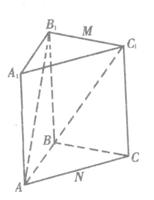，AB=4，BC=4，BB1=3，M、N分别是B1C1和AC的中点．

(Ⅰ)求异面直线AB1与BC1所成的角；

(Ⅱ)求MN的长；

(Ⅲ)求MN与底面ABC所成的角．

(Ⅰ)过C作CD∥AB，过A作AD∥CB，交CD于D，连结C1D，

∵B1C1∥BC，B1C1=BC，BC∥AD,BC=AD,

∴四边形ADB1C1为矩形，且AB1∥C1D，

∴∠BC1D为异面直线AB1与BC1所成的角或其补角.

由已知条件和余弦定理，∴cos∠BC1D=.

∴异面直线AB1与BC1所成的角为arccos. 

(Ⅱ)取BC的中点P，连结MP、NP，则MP∥BB1，

∴MP⊥面ABC，又NP面ABC，∴MP⊥NP.

PN=AB=2,MP=3,∴MN=

(Ⅲ)由(Ⅱ)知，

MN与底面所成的角为∠MNP，且NP=2，tan∠MNP=,∠MNP=arctan.

练习册系列答案
相关题目
精英家教网如图所示，直三棱柱ABC-A1B1C1的各条棱长均为a，D是侧棱CC1的中点．
（1）求证：平面AB1D⊥平面ABB1A1；
（2）求异面直线AB1与BC所成角的余弦值；
（3）求平面AB1D与平面ABC所成二面角（锐角）的大小．
如图所示，直三棱柱ABC-A1B1C1中，AB⊥AC，D，E分别为AA1，B1C的中点，若记
AB
=
a
，
AC
=
b
，
AA
=
c
，则
DE
=
1
2
a
+
1
2
b
1
2
a
+
1
2
b
（用
a
，
b
，
c
表示）．
如图所示，直三棱柱ABC-A'B'C'中，∠BCA=90°，CA=CB=1，AA'=2，M，N分别是A'B'、A'A的中点．
（1）求证：A'B⊥C'M；
（2）求异面直线BA'与CB'所成交的大小；
（3）（理）求BN与平面CNB'所称的角的大小；
（4）（理）求二面角A-BN-C的大小．
如图所示，直三棱柱ABC—A1B1C1中，底面是等腰直角三角形，∠ACB=90°,AC=1,AA1=,点D是AB的中点.

（1）求证：CD⊥平面ABB1A1；

（2）求二面角A-A1B-C的平面角的正切值;

（3）求三棱锥B1—A1BC的体积；

（4）求BC1与平面A1BC所成角的正弦值.
如图所示,在直三棱柱ABC—A1B1C1中,∠ABC=90°,D为棱AC的中点,且AB=BC=BB1=a.

(1)求证:AB1∥平面BC1D;

(2)求异面直线AB1与BC1所成的角;

(3)求点A到平面BC1D的距离.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网