题目内容
设函数f(x)=ax2+bx+k(k>0)在x=0处取得极值,且曲线y=f(x)在点(1,f(1))处的切线垂直于直线x+2y+1=0.
(Ⅰ)求a,b的值;
(Ⅱ)若函数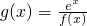 ,讨论g(x)的单调性.
,讨论g(x)的单调性.
解:(Ⅰ)因f(x)=ax2+bx+k(k>0),故f'(x)=2ax+b又f(x)在x=0处取得极限值,故f'(x)=0,从而b=0由曲线y=f(x)在(1,f(1))处的切线与直线x-2y+1=0相互垂直可知
该切线斜率为2,
即f'(1)=2,有2a=2,从而a=1(6分)
(Ⅱ)由(Ⅰ)知:
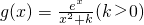 、
、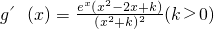
令g'(x)=0,有x2-2x+k=0(8分)
(1)当△=4-4k<0,即当k>1时,g'(x)>0在R上恒成立,故函数g(x)在R上为增函数(10分)
(2)当△=4-4k=0,即当k=1时,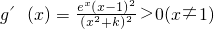 ,K=1时,g(x)在R上为增函数(12分)
,K=1时,g(x)在R上为增函数(12分)
(3)△=4-4k>0,即当0<k<1时,方程x2-2x+k=0有两个不相等实根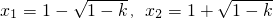
当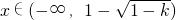 是g'(x)>0,故g(x)在
是g'(x)>0,故g(x)在 上为增函数
上为增函数
当 时,g'(x)<0,故g(x)在
时,g'(x)<0,故g(x)在 上为减函数
上为减函数
当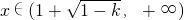 时,g'(x)>0,故g(x)在
时,g'(x)>0,故g(x)在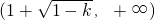 上为增函数(14分)
上为增函数(14分)
分析:(Ⅰ)因为”函数在x=0处取得极值“,则有f'(0)=0,再由“曲线y=f(x)在(1,f(1))处的切线与直线x-2y+1=0相互垂直”,则有f'(1)=2,从而求解.
(Ⅱ)由(Ⅰ)可得到: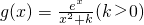 ,令g'(x)=0,有x2-2x+k=0,因为还有参数k,由一元二次方程,分三种情况讨论,(1)当△=4-4k<0,函数g(x)在R上为增函数,(2)当△=4-4k=0,g(x)在R上为增函数(3)△=4-4k>0,方程x2-2x+k=0有两个不相等实根,则由其两根来构建单调区间.
,令g'(x)=0,有x2-2x+k=0,因为还有参数k,由一元二次方程,分三种情况讨论,(1)当△=4-4k<0,函数g(x)在R上为增函数,(2)当△=4-4k=0,g(x)在R上为增函数(3)△=4-4k>0,方程x2-2x+k=0有两个不相等实根,则由其两根来构建单调区间.
点评:本题主要考查导数的几何意义,函数的极值及函数的单调性.综合性较强,充分考查了函数方程不等式三者的内在联系与转化.
该切线斜率为2,
即f'(1)=2,有2a=2,从而a=1(6分)
(Ⅱ)由(Ⅰ)知:
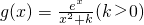 、
、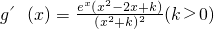
令g'(x)=0,有x2-2x+k=0(8分)
(1)当△=4-4k<0,即当k>1时,g'(x)>0在R上恒成立,故函数g(x)在R上为增函数(10分)
(2)当△=4-4k=0,即当k=1时,
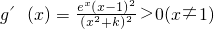 ,K=1时,g(x)在R上为增函数(12分)
,K=1时,g(x)在R上为增函数(12分)(3)△=4-4k>0,即当0<k<1时,方程x2-2x+k=0有两个不相等实根
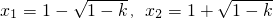
当
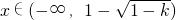 是g'(x)>0,故g(x)在
是g'(x)>0,故g(x)在 上为增函数
上为增函数当
 时,g'(x)<0,故g(x)在
时,g'(x)<0,故g(x)在 上为减函数
上为减函数当
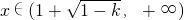 时,g'(x)>0,故g(x)在
时,g'(x)>0,故g(x)在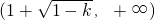 上为增函数(14分)
上为增函数(14分)分析:(Ⅰ)因为”函数在x=0处取得极值“,则有f'(0)=0,再由“曲线y=f(x)在(1,f(1))处的切线与直线x-2y+1=0相互垂直”,则有f'(1)=2,从而求解.
(Ⅱ)由(Ⅰ)可得到:
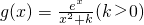 ,令g'(x)=0,有x2-2x+k=0,因为还有参数k,由一元二次方程,分三种情况讨论,(1)当△=4-4k<0,函数g(x)在R上为增函数,(2)当△=4-4k=0,g(x)在R上为增函数(3)△=4-4k>0,方程x2-2x+k=0有两个不相等实根,则由其两根来构建单调区间.
,令g'(x)=0,有x2-2x+k=0,因为还有参数k,由一元二次方程,分三种情况讨论,(1)当△=4-4k<0,函数g(x)在R上为增函数,(2)当△=4-4k=0,g(x)在R上为增函数(3)△=4-4k>0,方程x2-2x+k=0有两个不相等实根,则由其两根来构建单调区间.点评:本题主要考查导数的几何意义,函数的极值及函数的单调性.综合性较强,充分考查了函数方程不等式三者的内在联系与转化.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |