题目内容
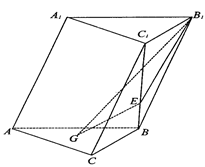
如图,四棱锥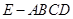 中,面
中,面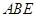
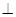 面
面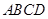 ,底面
,底面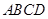 是直角梯形,侧面
是直角梯形,侧面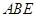 是等腰直角三角形.且
是等腰直角三角形.且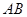 ∥
∥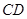 ,
,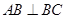 ,
,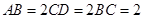 ,
,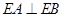 .
.
(1)判断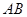 与
与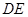 的位置关系;
的位置关系;
(2)求三棱锥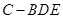 的体积;
的体积;
(3)若点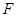 是线段
是线段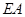 上一点,当
上一点,当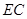 //平面
//平面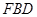 时,求
时,求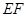 的长.
的长.
(1) ;(2)
;(2) ;(3)
;(3) .
.
解析试题分析:本题以四棱锥为几何背景考查线线垂直、线面垂直、线面平行、线线平行的判定,在解题过程中还遇到了等腰直角三角形和直角梯形以及相似三角形等基础知识,考查空间想象能力和推理论证能力.第一问,取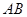 中点
中点 ,连结
,连结 ,因为
,因为 是等腰直角三角形,所以
是等腰直角三角形,所以 ,因为
,因为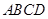 是直角梯形且
是直角梯形且 ,所以四边形
,所以四边形 为正方形,所以
为正方形,所以 ,所以
,所以 平面
平面 ,所以
,所以 ;第二问,先利用面面垂直,可得到线面垂直,得到锥体的高
;第二问,先利用面面垂直,可得到线面垂直,得到锥体的高 ,用等体积法将
,用等体积法将 转化为
转化为 ,再利用体积公式求值;第三问,先在面内找到线
,再利用体积公式求值;第三问,先在面内找到线 ,这是由于
,这是由于 // 平面
// 平面 ,再利用相似三角形,得到边长的关系,所以
,再利用相似三角形,得到边长的关系,所以 ,所以
,所以 .
.
试题解析:(1)证明:取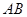 中点
中点 ,连结
,连结 ,
, .
.
因为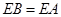 ,所以
,所以 .
.
因为四边形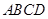 为直角梯形,
为直角梯形, ,
,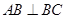 ,
,
所以四边形 为正方形,所以
为正方形,所以 .
.
所以 平面
平面 . 所以
. 所以  . 4分
. 4分
(2)由 ,面
,面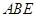
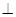 面
面 易得
易得
所以, 8分
8分
(3)解:连接 交于点,面
交于点,面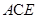
 面
面 .
.
因为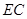 //平面
//平面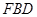 ,所以
,所以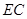 //
// .
.
在梯形 中,有
中,有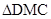 与
与 相似,
相似,
可得
所以,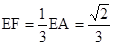 12分
12分
考点:1.线面垂直的判定定理;2.等体积法;3.相似三角形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的侧棱
的侧棱 两两垂直,且
两两垂直,且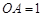 ,
,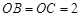 ,
,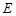 是
是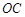 的中点。
的中点。
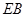 与
与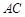 所成角的余弦值;
所成角的余弦值;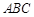 的所成角的正弦值。
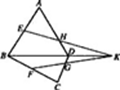
的所成角的正弦值。 中,
中, 是边长为2的正三角形,平面
是边长为2的正三角形,平面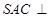 平面
平面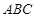 ,
,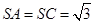 ,
, 分别为
分别为 的中点.
的中点.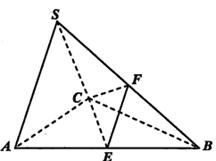
 ;
; 的余弦值;
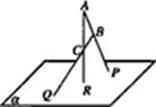
的余弦值;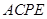 中,
中,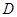 为
为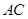 中点,
中点,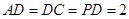 ,
,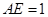 ,且
,且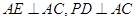 ,现沿
,现沿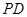 折起使
折起使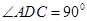 ,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.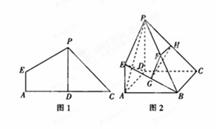
 的体积;
的体积; 与直线
与直线 所成角为
所成角为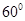 ?若存在,求出线段的长;若不存在,请说明理由.
?若存在,求出线段的长;若不存在,请说明理由.


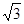 ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小