题目内容
设M为平面内一些向量组成的集合,若对任意正实数λ和向量a∈M,都有λa∈M,则称M为“点射域”,则下列平面向量的集合为“点射域”的是( )
| A.{(x,y)|y≥x2} | B.{(x,y)|
| |||||
| C.{(x,y)|x2+y2-2y≥0} | D.{(x,y)|3x2+2y2-12<0} |
根据“点射域”的定义,可得向量
∈M时,与它共线的向量λ
∈M也成立,
对于A,M={(x,y)|y≥x2}表示终点在抛物线y≥x2上及其张口以内的向量构成的区域,
向量
=(1,1)∈M,但3
=(3,3)∉M,故它不是“点射域”;
对于B,M={(x,y)|
},可得任意正实数λ和向量
∈M,都有λ
∈M,故它是“点射域”;
对于C,M={(x,y)|x2+y2-2y≥0},表示终点在圆x2+y2-2y=0上及其外部的向量构成的区域,
向量
=(0,2)∈M,但
=(0,1)∉M,故它不是“点射域”;
对于D,M={(x,y)|3x2+2y2-12<0},表示终点在椭圆 3x2+2y2=12的向量构成的区域,
向量
=(1,1)∈M,但3
=(3,3)∉M,故它不是“点射域”.
综上所述,满足是“点射域”的区域只有B
故选B.
| a |
| a |
对于A,M={(x,y)|y≥x2}表示终点在抛物线y≥x2上及其张口以内的向量构成的区域,
向量
| a |
| a |
对于B,M={(x,y)|
|
| a |
| a |
对于C,M={(x,y)|x2+y2-2y≥0},表示终点在圆x2+y2-2y=0上及其外部的向量构成的区域,
向量
| a |
| 1 |
| 2 |
| a |
对于D,M={(x,y)|3x2+2y2-12<0},表示终点在椭圆 3x2+2y2=12的向量构成的区域,
向量
| a |
| a |
综上所述,满足是“点射域”的区域只有B
故选B.

练习册系列答案
相关题目
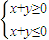 };
};