题目内容
已知函数f(x)=ax2+a2x+2b-a3,当x∈(-2,6)时,其值为正,而当x∈(-∞,-2)∪(6,+∞)时,其值为负,
(Ⅰ)求实数a,b的值及函数f(x)的表达式;
(Ⅱ)设F(x)= f(x)+4(k+1)x+2(6k-1),问k取何值时,函数F(x)的值恒为负值?
f(x)+4(k+1)x+2(6k-1),问k取何值时,函数F(x)的值恒为负值?
(Ⅰ)求实数a,b的值及函数f(x)的表达式;
(Ⅱ)设F(x)=
 f(x)+4(k+1)x+2(6k-1),问k取何值时,函数F(x)的值恒为负值?
f(x)+4(k+1)x+2(6k-1),问k取何值时,函数F(x)的值恒为负值? 解:(1)由题意可知-2和6是方程f(x)=0的两根,
∴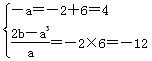 ,
,
∴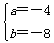 ,
,
∴f(x)=-4x2+16x+48;
(2)F(x)=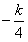 (-4x2+16x+48)+4(k+1)x+2(6k-1)=kx2+4x-2,
(-4x2+16x+48)+4(k+1)x+2(6k-1)=kx2+4x-2,
当k=0时,F(x)=4x-2不恒为负值;
当k≠0时,若F(x)的值恒为负值,
则有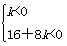 ,解得k<-2。
,解得k<-2。
∴
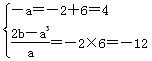 ,
,∴
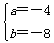 ,
,∴f(x)=-4x2+16x+48;
(2)F(x)=
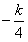 (-4x2+16x+48)+4(k+1)x+2(6k-1)=kx2+4x-2,
(-4x2+16x+48)+4(k+1)x+2(6k-1)=kx2+4x-2,当k=0时,F(x)=4x-2不恒为负值;
当k≠0时,若F(x)的值恒为负值,
则有
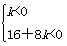 ,解得k<-2。
,解得k<-2。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目