题目内容
已知函数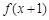 是偶函数,当
是偶函数,当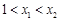 时,
时, 恒成立,设
恒成立,设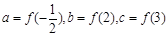 ,则
,则 的大小关系为 ( )
的大小关系为 ( )
A.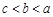 | B.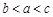 | C.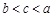 | D.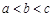 |
B
解析试题分析:因为当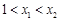 时,
时, 恒成立,所以根据函数单调性的定义可知该函数在
恒成立,所以根据函数单调性的定义可知该函数在 上单调递增,又因为函数
上单调递增,又因为函数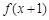 是偶函数,所以函数关于直线
是偶函数,所以函数关于直线 对称,所以
对称,所以 ,所以
,所以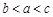 .
.
考点:本小题主要考查函数单调性和奇偶性的应用.
点评:函数的单调性、奇偶性、周期性、对称性等都是函数的比较重要的性质,要灵活应用.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
对于函数 (其中
(其中 ),选取
),选取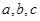 的一组值计算
的一组值计算 和
和 ,所得出的正确结果一定不可能的是 ( )
,所得出的正确结果一定不可能的是 ( )
| A.4和6 | B.3和1 | C.2和4 | D.1和2 |
设函数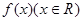 满足
满足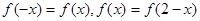 ,且当
,且当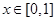 时,
时,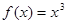 .又函数
.又函数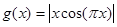 ,则函数
,则函数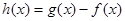 在
在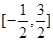 上的零点个数为 ( )
上的零点个数为 ( )
| A.5 | B. 6 | C.7 | D.8 |
在函数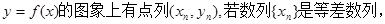 数列{
数列{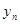 }是等比数列,则函数
}是等比数列,则函数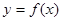 的解析式可能为( )
的解析式可能为( )
A.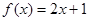 | B.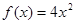 |
C.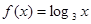 | D.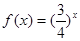 |
 的值属于区间
的值属于区间
A. | B. | C. | D. |
已知函数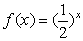 ,则函数
,则函数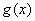 的图象与
的图象与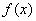 的图象关于直线
的图象关于直线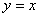 对称,则函数
对称,则函数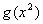 是( )
是( )
A.奇函数在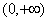 上单调递减 上单调递减 | B.偶函数在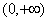 上单调递增 上单调递增 |
C.奇函数在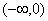 上单调递减 上单调递减 | D.偶函数在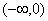 上单调递增 上单调递增 |
下列函数中,与函数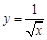 有相同定义域的是
有相同定义域的是
A.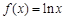 | B.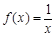 | C.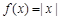 | D.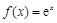 |
下列函数中,与函数 相同的函数是 ( )
相同的函数是 ( )
A. | B. | C. | D. |
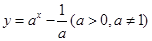 的图象可能是 ( )
的图象可能是 ( )