题目内容
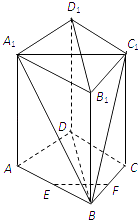
【题目】如图1,在边长为3的正三角形中, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 上的点,且满足
上的点,且满足![]() .将
.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,连结
,连结![]() ,
, ![]() ,
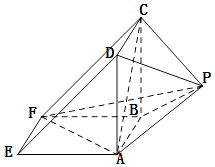
, ![]() .(如图2)
.(如图2)
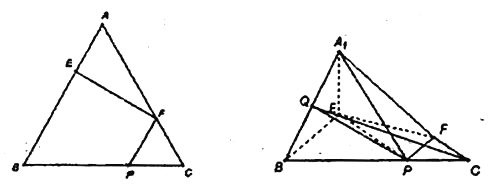
(Ⅰ)若![]() 为
为![]() 中点,求证:
中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)求![]() 与平面
与平面![]() 所成角的正切.
所成角的正切.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() ,
, ![]() .由三角中位线可证四边形
.由三角中位线可证四边形![]() 为平行四边形,则
为平行四边形,则![]() ,再由线线平行到线面平行;(Ⅱ)取
,再由线线平行到线面平行;(Ⅱ)取![]() 中点
中点![]() ,连结
,连结![]() ,由所给数据可证平面
,由所给数据可证平面![]() 平面
平面![]() ,再由面面垂直,线面垂直的性质可得
,再由面面垂直,线面垂直的性质可得![]() ;(Ⅲ)作
;(Ⅲ)作![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() ,可得
,可得![]() 为
为![]() 与平面
与平面![]() 所成角,可求其正切值.
所成角,可求其正切值.
试题解析:证明:(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() ,
, ![]() .
.
在![]() 中,
中, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,
所以![]() ,且
,且![]() .
.
因为![]() ,
,
所以![]() ,且
,且![]() ,
,
所以![]() ,
, ![]() .
.
所以四边形![]() 为平行四边形.
为平行四边形.
所以![]() .
.
又因为![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.

(Ⅱ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
因为![]() ,
, ![]() ,
,
∴![]() ,
,
而![]() ,即
,即![]() 是正三角形.
是正三角形.
又因为![]() ,所以
,所以![]() .
.
所以在图2有![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() 所以
所以![]() 平面
平面![]() 由
由![]() 平面
平面![]() 所以
所以![]()
(Ⅲ)作![]() 于
于![]() ,连接
,连接![]() ,则
,则![]()
因为![]() ,
, ![]() ,
, ![]() ,因此
,因此![]() 平面
平面![]() ,
,
因此![]() 平面
平面![]() ,因此
,因此![]() 是
是![]() 在平面
在平面![]() 内的射影,
内的射影,
因此![]() 为
为![]() 与平面
与平面![]() 所成角,
所成角,
![]() ,
, ![]() ,
, ![]()
![]() 中,
中, ![]() ,于是
,于是![]()
因此 ,
,
因此![]() 与平面
与平面![]() 所成角的正切为
所成角的正切为![]()


练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
【题目】2016年高一新生入学后,为了了解新生学业水平,某区对新生进行了水平测试,随机抽取了50名新生的成绩,其相关数据统计如下:
分数段 | 频数 | 选择题得分24分以上(含24分) |
| 5 | 2 |
| 10 | 4 |
| 15 | 12 |
| 10 | 6 |
| 5 | 4 |
| 5 | 5 |
(Ⅰ)若从分数在![]() ,
, ![]() 的被调查的新生中各随机选取2人进行追踪调查,求恰好有2名新生选择题得分不足24分的概率;
的被调查的新生中各随机选取2人进行追踪调查,求恰好有2名新生选择题得分不足24分的概率;
(Ⅱ)在(Ⅰ)的条件下,记选中的4名新生中选择题得分不足24分的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.