题目内容
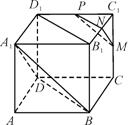
在正方体ABCD—A1B1C1D1中，M、N、P分别是C1C、B1C1、C1D1的中点，____________________.（先在横线上填上一个结论，然后再证明）构建问题：正方形ABCD—A1B1C1D1中，M、N、P分别是C1C、B1C1、C1D1的中点，试证明平面MNP∥平面A1BD.
思路分析：要证明面MNP∥面A1BD，只需证明两平面内有两条相交直线分别平行即可.
解：连结B1D1，∵P、N分别是D1C1、B1C1的中点，∴PN∥B1D1.
又B1D1∥BD，∴PN∥BD.
又PN
平面A1BD，∴PN∥平面A1BD.
同理，MN∥平面A1BD.
又PN∩MN=N，
∴平面PMN∥平面A1BD.
练习册系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）