题目内容
已知函数 则{x|f(x)>2}=________.
则{x|f(x)>2}=________.
(-∞,-1)∪(2,+∞)
分析:由题意需要分两种情况求解:x≤1时和x>1时,代入解析式列出方程,利用二次不等式的解法和对数的单调性求解,最后要把结果并起来.
解答:由题意分两种情况求解f(x)>2:
当x≤1时,x2-x>2,即x2-x-2>0,解得x>2或x<-1,
即x<-1,
当x>1时,2 >2,即
>2,即 >1,解得x>2,
>1,解得x>2,
即x>2,
综上得,不等式的解集是(-∞,-1)∪(2,+∞).
故答案为:(-∞,-1)∪(2,+∞).
点评:本题考查了分段函数求值问题,以及二次不等式的解法和对数的单调性应用,考查了分类讨论思想.
分析:由题意需要分两种情况求解:x≤1时和x>1时,代入解析式列出方程,利用二次不等式的解法和对数的单调性求解,最后要把结果并起来.
解答:由题意分两种情况求解f(x)>2:
当x≤1时,x2-x>2,即x2-x-2>0,解得x>2或x<-1,
即x<-1,
当x>1时,2
 >2,即
>2,即 >1,解得x>2,
>1,解得x>2,即x>2,
综上得,不等式的解集是(-∞,-1)∪(2,+∞).
故答案为:(-∞,-1)∪(2,+∞).
点评:本题考查了分段函数求值问题,以及二次不等式的解法和对数的单调性应用,考查了分类讨论思想.

练习册系列答案
相关题目
 则{x|f(x)>2}= .
则{x|f(x)>2}= .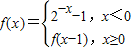 则满足f(x)=1的实数x的集合是 .
则满足f(x)=1的实数x的集合是 .