Question

【题目】已知函数，则下列结论正确的有( )

A. 函数的最大值为2；

B. 函数的图象关于点对称；

C. 函数的图象左移个单位可得函数的图象；

D. 函数的图象与函数的图象关于轴对称；

E. 若实数使得方程在上恰好有三个实数解，，，则一定有.

Answer 1

【答案】ACDE

【解析】

由正弦函数的最值可判断A；由对称中心解方程可判断B； 运用图象平移规律和函数奇偶性的性质，可判断C；运用函数图像的对称性，可判断D；运用图像可判断E.

由数可得最大值为2，故A对；

可令kπ，可得x＝kπ，k∈Z，

即有对称中心为（kπ，0），故B错；

f（x）的图象向左平移个单位可得y＝2sin（x），即y＝2sin（x），故C对；

与函数的图象关于x轴对称的函数为y=，故D对；又f（x）的对称轴为kπ，可得x＝kπ，k∈Z，

函数在上的大致图像：

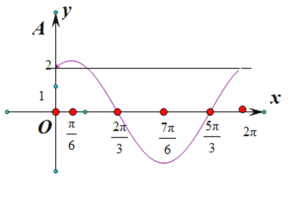
若使得方程在上恰好有三个实数解，，，则=0，+，

所以，故E对，

故选：ACDE．