题目内容
在平面内有n(n∈N*,n≥3)条直线,其中任何两条不平行,任何三条不过同一点,若这n条直线把平面分成f(n)个平面区域,则f(5)的值是 .f(n)的表达式是 .
【答案】分析:本题是一道推理问题.通过通过动手作图得,每一项与它前面一项的差构成一个等差数列,再结合类似于等差数列求通项的方法即可求出通项f(n),从而解决问题.
解答:解:通过动手作图,可知f(3)=7,f(4)=11,f(5)=16,
从中可归纳推理,得出f(n)=f(n-1)+n,则f(n)-f(n-1)=n,
f(n-1)-f(n-2)=n-1,
f(n-2)-f(n-3)=n-2,
…
f(5)-f(4)=5,
f(4)-f(3)=4,
将以上各式累加得:
f(n)-f(3)=n+(n-1)+(n-2)+…+5+4=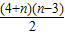 ,
,
则有f(n)=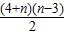 +f(3)=
+f(3)=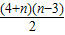 +7
+7
=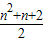 .
.
故答案为16;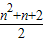 .
.
点评:题主要考查了归纳推理,以及数列递推式,属于基础题.所谓归纳推理,就是从个别性知识推出一般性结论的推理.
解答:解:通过动手作图,可知f(3)=7,f(4)=11,f(5)=16,
从中可归纳推理,得出f(n)=f(n-1)+n,则f(n)-f(n-1)=n,
f(n-1)-f(n-2)=n-1,
f(n-2)-f(n-3)=n-2,
…
f(5)-f(4)=5,
f(4)-f(3)=4,
将以上各式累加得:
f(n)-f(3)=n+(n-1)+(n-2)+…+5+4=
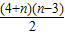 ,
,则有f(n)=
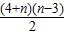 +f(3)=
+f(3)=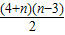 +7
+7=
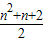 .
.故答案为16;
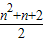 .
.点评:题主要考查了归纳推理,以及数列递推式,属于基础题.所谓归纳推理,就是从个别性知识推出一般性结论的推理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目