题目内容
设集合A={x|x2-3x+2=0},B={x|x2+2(a+1)x+(a2-5)=0}.(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
【答案】分析:(1)先解出集合A,根据2是两个集合的公共元素可知2∈B,建立关于a的等式关系,求出a后进行验证即可.
(2)一般A∪B=A转化成B⊆A来解决,集合A两个元素故可考虑对集合B的元素个数进行讨论求解.
解答:解:由x2-3x+2=0得x=1或x=2,故集合A={1,2}
(1)∵A∩B={2},∴2∈B,代入B中的方程,
得a2+4a+3=0⇒a=-1或a=-3;
当a=-1时,B={x|x2-4=0}={-2,2},满足条件;
当a=-3时,B={x|x2-4x+4=0}={2},满足条件;
综上,a的值为-1或-3;
(2)对于集合B,
△=4(a+1)2-4(a2-5)=8(a+3).
∵A∪B=A,∴B⊆A,
①当△<0,即a<-3时,B=∅满足条件;
②当△=0,即a=-3时,B={2},满足条件;
③当△>0,即a>-3时,B=A={1,2}才能满足条件,
则由根与系数的关系得
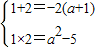 ⇒
⇒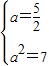 矛盾;
矛盾;
综上,a的取值范围是a≤-3.
点评:本题主要考查了交集并集以及一元二次方程的解法,属于基础题,考查分类讨论的思想.
(2)一般A∪B=A转化成B⊆A来解决,集合A两个元素故可考虑对集合B的元素个数进行讨论求解.
解答:解:由x2-3x+2=0得x=1或x=2,故集合A={1,2}
(1)∵A∩B={2},∴2∈B,代入B中的方程,
得a2+4a+3=0⇒a=-1或a=-3;
当a=-1时,B={x|x2-4=0}={-2,2},满足条件;
当a=-3时,B={x|x2-4x+4=0}={2},满足条件;
综上,a的值为-1或-3;
(2)对于集合B,
△=4(a+1)2-4(a2-5)=8(a+3).
∵A∪B=A,∴B⊆A,
①当△<0,即a<-3时,B=∅满足条件;
②当△=0,即a=-3时,B={2},满足条件;
③当△>0,即a>-3时,B=A={1,2}才能满足条件,
则由根与系数的关系得
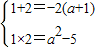 ⇒
⇒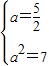 矛盾;
矛盾;综上,a的取值范围是a≤-3.
点评:本题主要考查了交集并集以及一元二次方程的解法,属于基础题,考查分类讨论的思想.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目