题目内容
把一个正方体的每个角沿各棱的中点都截去一个三棱锥,变成一个新的几何体,那么在新几何体中任意两个顶点连成直线段,则其位于正方体内部的概率为
- A.
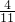
- B.
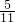
- C.
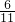
- D.

B
分析:根据题意,新得到的几何体有12个顶点,由组合数公式可得从中任取两点连成直线段的情况数目,再分析其中直线段位于正方体内部的情况:用间接法,新几何体在原正方体的一个侧面上有4个点,从中任取两点连成直线段直线段不在原正方体的内部,由组合数可得其条数,进而可得所有不在正方体的内部的直线段的条数,进而可得在正方体的内部的直线段的条数;由等可能事件的概率计算可得答案.
解答:根据题意,新得到的几何体有12个顶点,从中任取两点连成直线段,共有C122=66种情况,
其中原正方体的一个侧面上有4个点,从中任取两点连成直线段,有C42种情况,这些直线段不在原正方体的内部,
正方体共6个面,则不在原正方体的内部,即在其表面的有6×C42=36种情况;
则在正方体的内部的有66-36=30条;
则概率为 =
=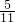 ;
;
故选B.
点评:本题考查等可能事件的概率,涉及正方体的结构特征;关键在于用间接法找到在正方体的内部的直线段的条数.
分析:根据题意,新得到的几何体有12个顶点,由组合数公式可得从中任取两点连成直线段的情况数目,再分析其中直线段位于正方体内部的情况:用间接法,新几何体在原正方体的一个侧面上有4个点,从中任取两点连成直线段直线段不在原正方体的内部,由组合数可得其条数,进而可得所有不在正方体的内部的直线段的条数,进而可得在正方体的内部的直线段的条数;由等可能事件的概率计算可得答案.
解答:根据题意,新得到的几何体有12个顶点,从中任取两点连成直线段,共有C122=66种情况,
其中原正方体的一个侧面上有4个点,从中任取两点连成直线段,有C42种情况,这些直线段不在原正方体的内部,
正方体共6个面,则不在原正方体的内部,即在其表面的有6×C42=36种情况;
则在正方体的内部的有66-36=30条;
则概率为
 =
=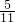 ;
;故选B.
点评:本题考查等可能事件的概率,涉及正方体的结构特征;关键在于用间接法找到在正方体的内部的直线段的条数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



