题目内容
若焦点在y轴上的椭圆
+
=1的离心率e=
,则m=
.
| x2 |
| 2 |
| y2 |
| m |
| 1 |
| 2 |
| 8 |
| 3 |
| 8 |
| 3 |
分析:由题意求出长半轴,半焦距,利用离心率求出m的值即可.
解答:解:因为焦点在y轴上的椭圆
+
=1,所以a=
,b=
,c=
,
因为e=
,∴
=
,
所以m=
.
故答案为:
.
| x2 |
| 2 |
| y2 |
| m |
| m |
| 2 |
| m-2 |
因为e=
| 1 |
| 2 |
| ||
|
| 1 |
| 2 |
所以m=
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:本题是基础题,考查椭圆的基本知识,注意椭圆的焦点所在的轴是解题的一个关键,否则容易错误.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
若焦点在y轴上的椭圆
+
=1的离心率为
,则m=( )
| x2 |
| m |
| y2 |
| 4 |
| ||
| 2 |
| A、1 | ||
| B、16 | ||
| C、1或16 | ||
D、
|
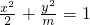 的离心率
的离心率 ,则m=________.
,则m=________. 的离心率
的离心率 ,则m= .
,则m= . 的离心率为
的离心率为 ,则m=( )
,则m=( )