题目内容
假设两圆互相外切,求证:用连心线做直径的圆,必与前两圆的外公切线相切.
证明:设⊙O1及⊙O2为互相外切的两个圆,其一外公切线为A1A2,
切点为A1及A2令点O为连心线O1O2的中点,过O作OA⊥A1A2,
由直角梯形的中位线性质得:OA= (O1A1+O2A2)=
(O1A1+O2A2)= O1O2,
O1O2,
∴以O1O2为直径,即以O为圆心,OA为半径的圆必与直线A1A2相切,
同理可证,此圆必切于⊙O1及⊙O2的另一条外公切线.
分析:设切点为A1及A2 ,令点O为连心线O1O2的中点,过O作OA⊥A1A2,由直角梯形的中位线性质得:OA= (O1A1+O2A2)=
(O1A1+O2A2)= O1O2 ,故以OA为半径的圆必与直线A1A2相切.
O1O2 ,故以OA为半径的圆必与直线A1A2相切.
点评:本题考查两个圆相外切的性质,圆的切线性质,以及梯形的中位线的性质的应用.
切点为A1及A2令点O为连心线O1O2的中点,过O作OA⊥A1A2,
由直角梯形的中位线性质得:OA=
 (O1A1+O2A2)=
(O1A1+O2A2)= O1O2,
O1O2,∴以O1O2为直径,即以O为圆心,OA为半径的圆必与直线A1A2相切,
同理可证,此圆必切于⊙O1及⊙O2的另一条外公切线.
分析:设切点为A1及A2 ,令点O为连心线O1O2的中点,过O作OA⊥A1A2,由直角梯形的中位线性质得:OA=
 (O1A1+O2A2)=
(O1A1+O2A2)= O1O2 ,故以OA为半径的圆必与直线A1A2相切.
O1O2 ,故以OA为半径的圆必与直线A1A2相切.点评:本题考查两个圆相外切的性质,圆的切线性质,以及梯形的中位线的性质的应用.

练习册系列答案
相关题目
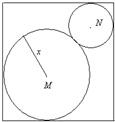 如图,在矩形ABCD内,两个圆M、N分别与矩形两边相切,且两圆互相外切.若矩形的长和宽分别为9和8,试把两个圆的面积之和S表示为圆M半径x的函数关系式,并求S的最大值和最小值.
如图,在矩形ABCD内,两个圆M、N分别与矩形两边相切,且两圆互相外切.若矩形的长和宽分别为9和8,试把两个圆的面积之和S表示为圆M半径x的函数关系式,并求S的最大值和最小值.