题目内容
若实数x、y满足方程x2＋y2＋8x－6y＋16＝0，则x2＋y2的最大值是________．
答案：64
解析：
解析：
x2＋y2＋8x－6y＋16＝0
(x＋4)2＋(y－3)2＝9，表示以(－4，3)为圆心，以3为半径的圆；x2＋y2表示点P(x，y)到原点的距离的平方．由圆心(－4，3)到原点的距离为5知点P(x，y)到原点距离的最大值为8，故x2＋y2的最大值是64．
练习册系列答案
阅读快车系列答案
相关题目
的最小值是
的最大值是．
的取值范围是（ ）
，
]
]∪[
，+∞）
]∪[
，+∞）
，
]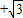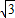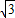