题目内容
已知函数
的最大值为
，其图像相邻两条对称轴之间的距离为
.
（Ⅰ）求函数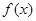
的解析式；
（Ⅱ）设
，求
的值．
（Ⅰ）y＝2sin(2x－
)＋1；（Ⅱ）
.
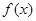解析试题分析：（Ⅰ）通过最大值为3可以求出A，再通过图像相邻两条对称轴之间的距离为可以得到周期，从而得到ω＝2，即得到函数的解析式；（Ⅱ）由，得到sin
＝
，结合
的范围，由
利用两角和的余弦公式即可得到本题答案.
试题解析：（Ⅰ）∵函数f(x)的最大值为3，∴A＋1＝3，即A＝2，
∵函数图像的相邻两条对称轴之间的距离为，∴最小正周期T＝π，∴ω＝2，
故函数f(x)的解析式为y＝2sin(2x－)＋1. 6分
（Ⅱ）∵f
＝2sin＋1＝
，即sin＝，
∵0<α<，∴－<α－<
,
∴
.
考点：1.
的图像与性质；2.三角恒等变换.
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
；
为第二象限角，化简
.
为钝角的的三角形
内角
的对边分别为
、
、
，
，且
与
垂直．
的取值范围
中，角A，B，C所对的边分别为
，
，求
的值．
的顶点在原点，始边与x轴正半轴重合，终边为射线4x＋3y＝0（x≥0），求5sin
．其中
．
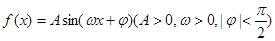的图象的一部分如下图所示.
的解析式；
时，求函数
的最大值与最小值及相应的
的值．
，
. 
的取值范围；
，试问当
变化时，
有没有最小值，如果有，求出这个最小值，如果没有，说明理由.
中，角
的对边分别为
，
.
的大小；
的值域
，
，且
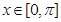的单调增区间；
为何值，直线
与函数