题目内容
已知椭圆E: +
+ =1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为
=1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为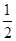 .
.
(1)求椭圆E的方程;
(2)若F为椭圆E的左焦点,O为坐标原点,直线l:y=kx+m与椭圆E相交于A、B两点,与直线x=-4相交于Q点,P是椭圆E上一点且满足 =
= +
+ ,证明
,证明 ·
· 为定值,并求出该值.
为定值,并求出该值.
(1) +
+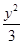 =1 (2)
=1 (2) ,证明见解析
,证明见解析
解析解:(1)抛物线y2=8x的焦点为(2,0),
又椭圆以抛物线焦点为顶点,
∴a=2,
又e=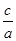 =
=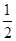 ,
,
∴c=1,∴b2=3.
∴椭圆E的方程为 +
+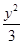 =1.
=1.
(2)由(1)知,F(-1,0),
由
消去y,得(3+4k2)x2+8kmx+4m2-12=0.
∵l与椭圆交于两点,
∴Δ=(8km)2-4(3+4k2)(4m2-12)>0,
即m2<4k2+3.
设A(x1,y1),B(x2,y2),
则x1、x2是上述方程的两个根,
∴x1+x2=- ,x1·x2=
,x1·x2= ,
,
又y1+y2=kx1+m+kx2+m
=k(x1+x2)+2m
=
∴ =
= +
+ =(-
=(- ,
, ),
),
由点P在椭圆上,得 +
+ =1.
=1.
整理得4m2=3+4k2,
又Q(-4,-4k+m),
∴ =(-3,-4k+m).
=(-3,-4k+m).
∴ ·
· =(-
=(- ,
, )·(-3,m-4k)
)·(-3,m-4k)
= +
+
=
= .
.
即 ·
· 为定值
为定值 .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
 )和
)和 ,并且经过点
,并且经过点 ,抛物线的顶点E在坐标原点,焦点恰好是椭圆C的右顶点F.
,抛物线的顶点E在坐标原点,焦点恰好是椭圆C的右顶点F. 的最小值.
的最小值. ,且
,且 .
. 的轨迹
的轨迹 的方程;
的方程; ,若斜率为
,若斜率为 的直线
的直线 过点
过点 并与轨迹
并与轨迹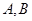 ,且对于轨迹
,且对于轨迹 ,都存在
,都存在 ,使得
,使得 成立,试求出满足条件的实数
成立,试求出满足条件的实数 的值.
的值. 直线
直线 与抛物线
与抛物线 没有交点;
没有交点; 方程
方程 表示椭圆;若
表示椭圆;若 为真命题,试求实数
为真命题,试求实数 的取值范围.
的取值范围.


 、
、 (
( )连线的斜率之积等于非零常数m的点的轨迹,加上
)连线的斜率之积等于非零常数m的点的轨迹,加上 、
、 两点所成的曲线C可以是圆、椭圆或双曲线.求曲线C的方程,并讨论C的形状与m值得关系.
两点所成的曲线C可以是圆、椭圆或双曲线.求曲线C的方程,并讨论C的形状与m值得关系. =
= .
.