题目内容
定义在R上的函数f(x)满足对于任意实数x,y都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(1)=-2.(1)判断f(x)的奇偶性并证明;
(2)判断f(x)的单调性,并求当x∈[-3,3]时,f(x)的最大值及最小值;
(3)在b>
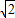 的条件下解关于x的不等式
的条件下解关于x的不等式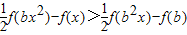 .
.
【答案】分析:(1)可在恒等式中令x=y=0,即可解出f(0)=0,由奇函数的定义知,需要证明出f(-x)=-f(x),观察恒等式发现若令y=-x,则问题迎刃而解;
(2)由题设条件对任意x1、x2在所给区间内比较f(x2)-f(x1)与0的大小即可得出f(x)在R上是减函数,再根据单调性得出函数的最值即可.
(3)不等式可化为: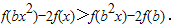 再利用题中条件得到2f(x)=f(x)+f(x)=f(2x),结合函数的单调性,将前不等式化成二次不等式,再解之即得.
再利用题中条件得到2f(x)=f(x)+f(x)=f(2x),结合函数的单调性,将前不等式化成二次不等式,再解之即得.
解答:解:(1)令x=y=0,得f(0)=f(0)+f(0),∴f(0)=0.…(1分)
再令y=-x,得f(0)=f(x)+f(-x)=0.∴f(-x)=-f(x).
∴f(x)为奇函数.…(3分)
(2)任取x1<x2,则x2-x1>0.∴由已知得f(x2-x1)<0.
∴f(x1)-f(x2)=f(x1)+f(-x2)=f(x1-x2)=-f(x2-x1)>0.
∴f(x1)>f(x2),∴f(x)在R上是减函数.…(6分)
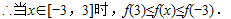
∵f(3)=f(2)+f(1)=3f(1)=-6,
∴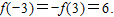
∴当x∈[-3,3]时,f(x)max=6,f(x)min=-6.…(8分)
(3)不等式可化为: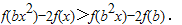
而2f(x)=f(x)+f(x)=f(2x),
得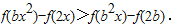
即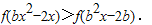
∵y=f(x)在R上是减函数,
∴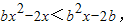 即bx2-(2+b2)x+2b<0…①…(10分)
即bx2-(2+b2)x+2b<0…①…(10分)
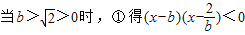 ;
;
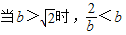 ,此时解集为{
,此时解集为{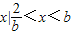 }.…(12分)
}.…(12分)
点评:本题考点是抽象函数及其应用,考查用赋值法求函数值证明函数的奇偶性,以及灵活利用所给的恒等式证明函数的单调性,此类题要求答题者有较高的数学思辨能力,能从所给的条件中组织出证明问题的组合来.
(2)由题设条件对任意x1、x2在所给区间内比较f(x2)-f(x1)与0的大小即可得出f(x)在R上是减函数,再根据单调性得出函数的最值即可.
(3)不等式可化为:
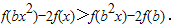 再利用题中条件得到2f(x)=f(x)+f(x)=f(2x),结合函数的单调性,将前不等式化成二次不等式,再解之即得.
再利用题中条件得到2f(x)=f(x)+f(x)=f(2x),结合函数的单调性,将前不等式化成二次不等式,再解之即得.解答:解:(1)令x=y=0,得f(0)=f(0)+f(0),∴f(0)=0.…(1分)
再令y=-x,得f(0)=f(x)+f(-x)=0.∴f(-x)=-f(x).
∴f(x)为奇函数.…(3分)
(2)任取x1<x2,则x2-x1>0.∴由已知得f(x2-x1)<0.
∴f(x1)-f(x2)=f(x1)+f(-x2)=f(x1-x2)=-f(x2-x1)>0.
∴f(x1)>f(x2),∴f(x)在R上是减函数.…(6分)
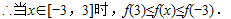
∵f(3)=f(2)+f(1)=3f(1)=-6,
∴
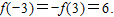
∴当x∈[-3,3]时,f(x)max=6,f(x)min=-6.…(8分)
(3)不等式可化为:
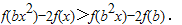
而2f(x)=f(x)+f(x)=f(2x),
得
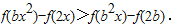
即
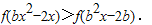
∵y=f(x)在R上是减函数,
∴
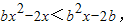 即bx2-(2+b2)x+2b<0…①…(10分)
即bx2-(2+b2)x+2b<0…①…(10分)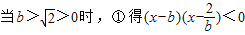 ;
;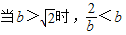 ,此时解集为{
,此时解集为{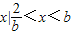 }.…(12分)
}.…(12分)点评:本题考点是抽象函数及其应用,考查用赋值法求函数值证明函数的奇偶性,以及灵活利用所给的恒等式证明函数的单调性,此类题要求答题者有较高的数学思辨能力,能从所给的条件中组织出证明问题的组合来.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目