题目内容
对于函数f1(x),f2(x),h(x),如果存在实数a,b使得h(x)=a•f1(x)+b•f2(x),那么称h(x)为f1(x),f2(x)的生成函数.
(Ⅰ)下面给出两组函数,h(x)是否分别为f1(x),f2(x)的生成函数?并说明理由;
第一组: ;
;
第二组:f1(x)=x2-x,f2(x)=x2+x+1,h(x)=x2-x+1;
(Ⅱ)设 ,生成函数h(x).若不等式3h2(x)+2h(x)+t<0在x∈[2,4]上有解,求实数t的取值范围;
,生成函数h(x).若不等式3h2(x)+2h(x)+t<0在x∈[2,4]上有解,求实数t的取值范围;
(Ⅲ)设 ,取a=1,b>0,生成函数h(x)使h(x)≥b恒成立,求b的取值范围.
,取a=1,b>0,生成函数h(x)使h(x)≥b恒成立,求b的取值范围.
解:(Ⅰ)①设 ,即
,即 ,
,
取 ,所以h(x)是f1(x),f2(x)的生成函数.(2分)
,所以h(x)是f1(x),f2(x)的生成函数.(2分)
②设a(x2+x)+b(x2+x+1)=x2-x+1,即(a+b)x2+(a+b)x+b=x2-x+1,
则 ,该方程组无解.
,该方程组无解.
所以h(x)不是f1(x),f2(x)的生成函数.(4分)
(Ⅱ) (5分)
(5分)
若不等式3h2(x)+2h(x)+t<0在x∈[2,4]上有解,
3h2(x)+2h(x)+t<0,即t<-3h2(x)-2h(x)=-3log22x-2log2x(7分)
设s=log2x,则s∈[1,2],y=-3log22x-2log2x=-3s2-2s,(9分)
ymax=-5,故,t<-5.(10分)
(Ⅲ)由题意,得
1°若 ,则h(x)在
,则h(x)在 上递减,在
上递减,在 上递增,
上递增,
则 ,
,
所以 ,得1≤b≤4(12分)
,得1≤b≤4(12分)
2°若 ,则h(x)在[1,10]上递增,则hmin=h(1)=1+b,
,则h(x)在[1,10]上递增,则hmin=h(1)=1+b,
所以 ,得0<b≤1.(14分)
,得0<b≤1.(14分)
3°若 ,则h(x)在[1,10]上递减,则
,则h(x)在[1,10]上递减,则 ,故
,故 ,无解
,无解
综上可知,0<b≤4.(16分)
分析:(Ⅰ)化简h(x)=a•f1(x)+b•f2(x),使得与 相同,求出a,b判断结果满足题意;类似方法计算判断第二组.
相同,求出a,b判断结果满足题意;类似方法计算判断第二组.
(Ⅱ)设 ,生成函数
,生成函数 .化简不等式3h2(x)+2h(x)+t<0,在x∈[2,4]上有解,就是求t<-3h2(x)-2h(x)=-3log22x-2log2x的最小值,即可.
.化简不等式3h2(x)+2h(x)+t<0,在x∈[2,4]上有解,就是求t<-3h2(x)-2h(x)=-3log22x-2log2x的最小值,即可.
(Ⅲ)设 ,取a=1,b>0,生成函数
,取a=1,b>0,生成函数
使 恒成立,分类讨论
恒成立,分类讨论 ,求出b的取值范围.
,求出b的取值范围.
点评:本题考查其他不等式的解法,函数的概念及其构成要素,函数恒成立问题,考查值思想,分类讨论,计算能力,函数与方程的思想,是中档题.
 ,即
,即 ,
,取
 ,所以h(x)是f1(x),f2(x)的生成函数.(2分)
,所以h(x)是f1(x),f2(x)的生成函数.(2分)②设a(x2+x)+b(x2+x+1)=x2-x+1,即(a+b)x2+(a+b)x+b=x2-x+1,
则
 ,该方程组无解.
,该方程组无解.所以h(x)不是f1(x),f2(x)的生成函数.(4分)
(Ⅱ)
 (5分)
(5分)若不等式3h2(x)+2h(x)+t<0在x∈[2,4]上有解,
3h2(x)+2h(x)+t<0,即t<-3h2(x)-2h(x)=-3log22x-2log2x(7分)
设s=log2x,则s∈[1,2],y=-3log22x-2log2x=-3s2-2s,(9分)
ymax=-5,故,t<-5.(10分)
(Ⅲ)由题意,得

1°若
 ,则h(x)在
,则h(x)在 上递减,在
上递减,在 上递增,
上递增,则
 ,
,所以
 ,得1≤b≤4(12分)
,得1≤b≤4(12分)2°若
 ,则h(x)在[1,10]上递增,则hmin=h(1)=1+b,
,则h(x)在[1,10]上递增,则hmin=h(1)=1+b,所以
 ,得0<b≤1.(14分)
,得0<b≤1.(14分)3°若
 ,则h(x)在[1,10]上递减,则
,则h(x)在[1,10]上递减,则 ,故
,故 ,无解
,无解综上可知,0<b≤4.(16分)
分析:(Ⅰ)化简h(x)=a•f1(x)+b•f2(x),使得与
 相同,求出a,b判断结果满足题意;类似方法计算判断第二组.
相同,求出a,b判断结果满足题意;类似方法计算判断第二组.(Ⅱ)设
 ,生成函数
,生成函数 .化简不等式3h2(x)+2h(x)+t<0,在x∈[2,4]上有解,就是求t<-3h2(x)-2h(x)=-3log22x-2log2x的最小值,即可.
.化简不等式3h2(x)+2h(x)+t<0,在x∈[2,4]上有解,就是求t<-3h2(x)-2h(x)=-3log22x-2log2x的最小值,即可.(Ⅲ)设
 ,取a=1,b>0,生成函数
,取a=1,b>0,生成函数
使
 恒成立,分类讨论
恒成立,分类讨论 ,求出b的取值范围.
,求出b的取值范围.点评:本题考查其他不等式的解法,函数的概念及其构成要素,函数恒成立问题,考查值思想,分类讨论,计算能力,函数与方程的思想,是中档题.

练习册系列答案
相关题目
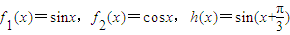 ;
;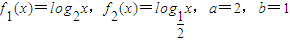 ,生成函数h(x).若不等式h(4x)+t•h(2x)<0在x∈[2,4]上有解,求实数t的取值范围.
,生成函数h(x).若不等式h(4x)+t•h(2x)<0在x∈[2,4]上有解,求实数t的取值范围.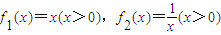 ,取a>0,b>0生成函数h(x)图象的最低点坐标为(2,8).若对于任意正实数x1,x2且x1+x2=1,试问是否存在最大的常数m,使h(x1)h(x2)≥m恒成立?如果存在,求出这个m的值;如果不存在,请说明理由.
,取a>0,b>0生成函数h(x)图象的最低点坐标为(2,8).若对于任意正实数x1,x2且x1+x2=1,试问是否存在最大的常数m,使h(x1)h(x2)≥m恒成立?如果存在,求出这个m的值;如果不存在,请说明理由.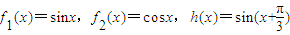 ;
;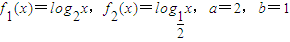 ,生成函数h(x).若不等式h(4x)+t•h(2x)<0在x∈[2,4]上有解,求实数t的取值范围.
,生成函数h(x).若不等式h(4x)+t•h(2x)<0在x∈[2,4]上有解,求实数t的取值范围.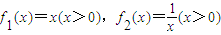 ,取a>0,b>0生成函数h(x)图象的最低点坐标为(2,8).若对于任意正实数x1,x2且x1+x2=1,试问是否存在最大的常数m,使h(x1)h(x2)≥m恒成立?如果存在,求出这个m的值;如果不存在,请说明理由.
,取a>0,b>0生成函数h(x)图象的最低点坐标为(2,8).若对于任意正实数x1,x2且x1+x2=1,试问是否存在最大的常数m,使h(x1)h(x2)≥m恒成立?如果存在,求出这个m的值;如果不存在,请说明理由.