题目内容
设O是△ABC的内切圆的圆心,|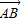 |=5,|
|=5,|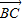 |=4,|
|=4,|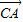 |=3,则下列结论正确的是( )
|=3,则下列结论正确的是( )A.
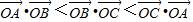
B.
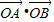 >
>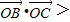
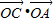
C.
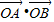 =
=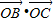 =
=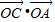
D.
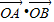 <
<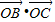 =
=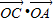
【答案】分析:由AB=5、BC=4、CA=3,我们易得△ABC是以C为直角的直角三角形,则根据数量积的意义,我们易得本题实际上是实数作差比大小,移项后结合分配律和向量数量积的运算性质,即可得到结论.
解答: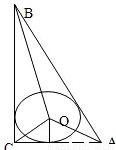 解:方法一(分析法)
解:方法一(分析法)
作出图形,如图,
∵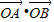 -
-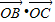 =
=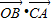 ,
,
由直角三角形C中为直角,
则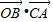 <0,
<0,
故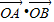 <
<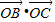 ;
;
同理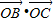 -
-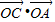 =
=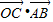 <0,
<0,
则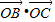 <
<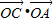 .
.
故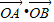 <
<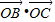 <
<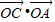 ,
,
方法二(坐标法)
以C为坐标原点建立直角坐标系,
∵O为△ABC的内切圆圆心,且AB=5、BC=4、CA=3,
∴C(0,0),O(1,1),A(3,0),B(0,4),
则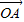 =(2,-1),
=(2,-1),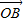 =(-1,3),
=(-1,3),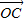 =(-1,-1)
=(-1,-1)
所以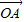 •
•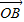 =-5,
=-5,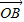 •
•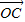 =-2,
=-2,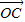 •
•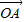 =-1,
=-1,
所以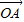 •
•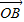 <
<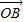 •
•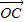 <
<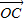 •
•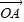
故选A.
点评:向量的数量积为实数可转化为实数大小的问题,作差借助减法的运算又化归数量积判断,借助几何条件判断数量积符号,充分显示了数量积的本质属性,为向量和实数的相互转化提供了方法和依据.
解答:
 解:方法一(分析法)
解:方法一(分析法)作出图形,如图,
∵
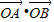 -
-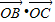 =
=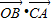 ,
,由直角三角形C中为直角,
则
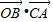 <0,
<0,故
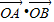 <
<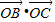 ;
;同理
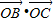 -
-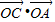 =
=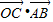 <0,
<0,则
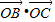 <
<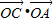 .
.故
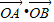 <
<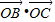 <
<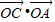 ,
,方法二(坐标法)
以C为坐标原点建立直角坐标系,
∵O为△ABC的内切圆圆心,且AB=5、BC=4、CA=3,
∴C(0,0),O(1,1),A(3,0),B(0,4),
则
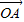 =(2,-1),
=(2,-1),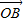 =(-1,3),
=(-1,3),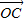 =(-1,-1)
=(-1,-1)所以
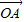 •
•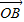 =-5,
=-5,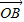 •
•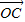 =-2,
=-2,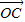 •
•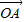 =-1,
=-1,所以
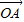 •
•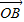 <
<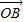 •
•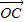 <
<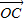 •
•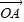
故选A.
点评:向量的数量积为实数可转化为实数大小的问题,作差借助减法的运算又化归数量积判断,借助几何条件判断数量积符号,充分显示了数量积的本质属性,为向量和实数的相互转化提供了方法和依据.

练习册系列答案
相关题目
 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2, C.
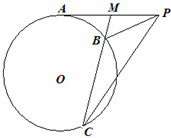
C. (1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.
(1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB. 表示的变换作用后,四边形ABCD变为四边形A1B1C1D1,问:四边形ABCD与四边形A1B1C1D1的面积是否相等?试证明你的结论.
表示的变换作用后,四边形ABCD变为四边形A1B1C1D1,问:四边形ABCD与四边形A1B1C1D1的面积是否相等?试证明你的结论. 上的动点,试求AB的最大值.
上的动点,试求AB的最大值. .
.
 表示的变换作用后,四边形ABCD变为四边形A1B1C1D1,问:四边形ABCD与四边形A1B1C1D1的面积是否相等?试证明你的结论.
表示的变换作用后,四边形ABCD变为四边形A1B1C1D1,问:四边形ABCD与四边形A1B1C1D1的面积是否相等?试证明你的结论.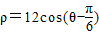 上的动点,试求AB的最大值.
上的动点,试求AB的最大值. .
.