题目内容
已知函数f(x)=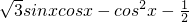
(1)求函数f(x)的单调减区间;
(2)若不等式|f(x)-m|<1对任意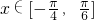 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
解:(1)∵sinxcosx= sin2x,cos2x=
sin2x,cos2x= (1+cos2x)
(1+cos2x)
∴f(x)=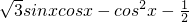
= sin2x-
sin2x- (1+cos2x)-
(1+cos2x)- =
= sin2x-
sin2x- cos2x-1=sin(2x-
cos2x-1=sin(2x- )-1
)-1
令 +2kπ≤2x-
+2kπ≤2x- ≤
≤ +2kπ,k∈Z
+2kπ,k∈Z
解得 +kπ≤x≤
+kπ≤x≤ +kπ,k∈Z
+kπ,k∈Z
∴函数f(x)的单调减区间为[ +kπ,
+kπ, +kπ],k∈Z
+kπ],k∈Z
(2)不等式|f(x)-m|<1,即-1+m<f(x)<1+m
∵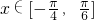 ,得2x-
,得2x- ∈[-
∈[- ,
, ]
]
∴-1≤sin(2x- )≤
)≤ ,得f(x)=sin(2x-
,得f(x)=sin(2x- )-1∈[-2,-
)-1∈[-2,- ]
]
∵不等式|f(x)-m|<1,对任意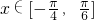 恒成立
恒成立
∴-2≥-1+m且1+m≥- ,解之得-
,解之得- ≤m≤-1
≤m≤-1
即实数m的取值范围是[- ,-1].
,-1].
分析:(1)根据二倍角三角函数公式和辅助角公式,将函数化简整理得f(x)=sin(2x- )-1,结合正弦函数单调区间的公式,解不等式即可得到函数f(x)的单调减区间;
)-1,结合正弦函数单调区间的公式,解不等式即可得到函数f(x)的单调减区间;
(2)设不等式|f(x)-m|<1的解集合是M,函数f(x)=sin(2x- )-1在区间
)-1在区间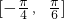 上的值域N,可得N是M的子集,由此建立关于m的不等式,解之即可得到实数m的取值范围.
上的值域N,可得N是M的子集,由此建立关于m的不等式,解之即可得到实数m的取值范围.
点评:本题给出三角函数式,要求我们将其化简成标准形式,并求函数的减区间,着重考查了三角恒等变形和三角函数的图象与性质等知识,属于中档题.
 sin2x,cos2x=
sin2x,cos2x= (1+cos2x)
(1+cos2x)∴f(x)=
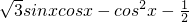
=
 sin2x-
sin2x- (1+cos2x)-
(1+cos2x)- =
= sin2x-
sin2x- cos2x-1=sin(2x-
cos2x-1=sin(2x- )-1
)-1令
 +2kπ≤2x-
+2kπ≤2x- ≤
≤ +2kπ,k∈Z
+2kπ,k∈Z解得
 +kπ≤x≤
+kπ≤x≤ +kπ,k∈Z
+kπ,k∈Z∴函数f(x)的单调减区间为[
 +kπ,
+kπ, +kπ],k∈Z
+kπ],k∈Z(2)不等式|f(x)-m|<1,即-1+m<f(x)<1+m
∵
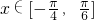 ,得2x-
,得2x- ∈[-
∈[- ,
, ]
]∴-1≤sin(2x-
 )≤
)≤ ,得f(x)=sin(2x-
,得f(x)=sin(2x- )-1∈[-2,-
)-1∈[-2,- ]
]∵不等式|f(x)-m|<1,对任意
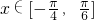 恒成立
恒成立∴-2≥-1+m且1+m≥-
 ,解之得-
,解之得- ≤m≤-1
≤m≤-1即实数m的取值范围是[-
 ,-1].
,-1].分析:(1)根据二倍角三角函数公式和辅助角公式,将函数化简整理得f(x)=sin(2x-
 )-1,结合正弦函数单调区间的公式,解不等式即可得到函数f(x)的单调减区间;
)-1,结合正弦函数单调区间的公式,解不等式即可得到函数f(x)的单调减区间;(2)设不等式|f(x)-m|<1的解集合是M,函数f(x)=sin(2x-
 )-1在区间
)-1在区间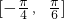 上的值域N,可得N是M的子集,由此建立关于m的不等式,解之即可得到实数m的取值范围.
上的值域N,可得N是M的子集,由此建立关于m的不等式,解之即可得到实数m的取值范围.点评:本题给出三角函数式,要求我们将其化简成标准形式,并求函数的减区间,着重考查了三角恒等变形和三角函数的图象与性质等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|