题目内容
已知函数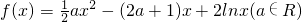
在x=1和x=3处的切线互相平行，则实数a=________．
分析：根据f（x）的解析式求出f（x）的导函数，因为曲线在x=1和x=3处的切线互相平行，得到切线的斜率相等，列出关于a的方程，求出方程的解即可得到a的值．
解答：由
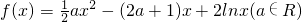，得到f′（x）=ax-（2a+1）+
，因为曲线在x=1和x=3处的切线互相平行，
所以f′（1）=f′（3），即a-（2a+1）+2=3a-（2a+1）+
，解得a=．故答案为：
．点评：此题考查学生会利用导数求曲线上过某点切线方程的斜率，掌握两直线平行时斜率的关系，是一道基础题．
练习册系列答案
相关题目
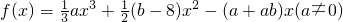在x=-3和x=2处取得极值，问：当c为何值时，不等式ax2+bx+c≤0在[1，4]上恒成立？
在x=1和x=3处的切线互相平行，则实数a= ．
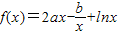在x=1和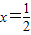
处取得极值．
上存在x，使得不等式f（x）-c≤0成立，求实数c的最小值．（参考数据e2≈7.389，e3≈20.08）
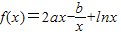在x=1和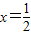
处取得极值．
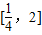上存在x，使得不等式f（x）-c≤0成立，求实数c的最小值．（参考数据e2≈7.389，e3≈20.08）