题目内容
设数列{an}满足a1=t,a2=t2,前n项和为Sn,且Sn+2-(t+1)Sn+1+tSn=0(n∈N*).
(1)证明数列{an}为等比数列,并求{an}的通项公式;
(2)当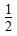 <t<2时,比较2n+2-n与tn+t-n的大小;
<t<2时,比较2n+2-n与tn+t-n的大小;
(3)若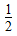 <t<2,bn=
<t<2,bn=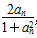 ,求证:
,求证: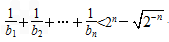
(1)证明数列{an}为等比数列,并求{an}的通项公式;
(2)当
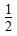 <t<2时,比较2n+2-n与tn+t-n的大小;
<t<2时,比较2n+2-n与tn+t-n的大小;(3)若
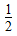 <t<2,bn=
<t<2,bn=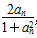 ,求证:
,求证: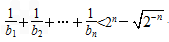
解:(1)证明:由Sn+2-(t+1)Sn+1+tSn=0,得tSn+1-tSn=Sn+2-Sn+1,即an+2=tan+1,而a1=t,a2=t2,
∴数列{an}是以t为首项,t为公比的等比数列,
∴an=tn.
(2)∵(tn+t-n)-(2n+2-n)=(tn-2n)[1-(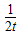 )n],又
)n],又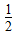 <t<2,
<t<2,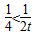 <1,
<1,
则tn-2n<0且1-(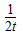 )n>0,
)n>0,
∴(tn-2n)[1-(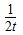 )n]<0,
)n]<0,
∴tn+t-n<2n+2-n.
(3)证明:∵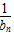 =
=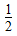 (tn+t-n),
(tn+t-n),
∴2(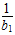 +
+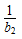 +…+
+…+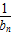 )<(2+22+…2n)+(2-1+2-2+…+2-n)=2(2n-1)+1-2-n
)<(2+22+…2n)+(2-1+2-2+…+2-n)=2(2n-1)+1-2-n
=2n+1-(1+2-n)<2n+1-2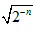 ,
,
∴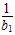 +
+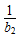 +…+
+…+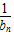 <2n-
<2n-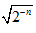
∴数列{an}是以t为首项,t为公比的等比数列,
∴an=tn.
(2)∵(tn+t-n)-(2n+2-n)=(tn-2n)[1-(
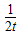 )n],又
)n],又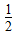 <t<2,
<t<2,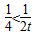 <1,
<1,则tn-2n<0且1-(
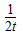 )n>0,
)n>0,∴(tn-2n)[1-(
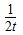 )n]<0,
)n]<0,∴tn+t-n<2n+2-n.
(3)证明:∵
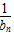 =
=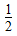 (tn+t-n),
(tn+t-n),∴2(
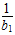 +
+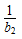 +…+
+…+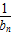 )<(2+22+…2n)+(2-1+2-2+…+2-n)=2(2n-1)+1-2-n
)<(2+22+…2n)+(2-1+2-2+…+2-n)=2(2n-1)+1-2-n=2n+1-(1+2-n)<2n+1-2
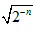 ,
,∴
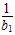 +
+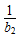 +…+
+…+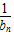 <2n-
<2n-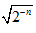

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
设数列{an}满足a1=1,a2+a4=6,且对任意n∈N*,函数f(x)=(an-an+1+an+2)x+an+1?cosx-an+2sinx满足f′(
)=0若cn=an+
,则数列{cn}的前n项和Sn为( )
| π |
| 2 |
| 1 |
| 2an |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|